题目内容
在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d.若战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为( )A.
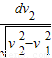
B.0
C.
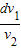
D.
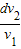
【答案】分析:将摩托艇的运动分解为沿河岸方向和垂直于河岸方向,当静水速的方向垂直于河岸时,渡河时间最短,根据垂直于河岸方向上位移和静水速求出运动时间,再根据水流速和时间求出沿河岸方向上的位移.
解答:解:当静水速与河岸垂直时,渡河时间最短.
t=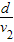
则摩托艇登陆的地点离O点的距离:x=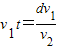 .故C正确,A、B、D错误.
.故C正确,A、B、D错误.
故选C.
点评:解决本题的关键知道分运动与合运动具有等时性,以及知道当静水速垂直于河岸时,渡河时间最短.
解答:解:当静水速与河岸垂直时,渡河时间最短.
t=
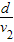
则摩托艇登陆的地点离O点的距离:x=
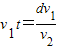 .故C正确,A、B、D错误.
.故C正确,A、B、D错误.故选C.
点评:解决本题的关键知道分运动与合运动具有等时性,以及知道当静水速垂直于河岸时,渡河时间最短.

练习册系列答案
相关题目
在一次抗洪抢险战斗中,一位武警战士驾船把群众送到河对岸的安全地方。设河水流速为3m/s,河宽为600m,船相对静水的速度为4m/s。则下列说法正确的是 ( )
| A.渡河的最短时间为120s |
| B.渡河的最短时间为150s |
| C.渡河的最短航程为600m |
| D.渡河的最短航程为750m |