题目内容
如图所示，A、B为一对平行板，板长为L，两板距离为d，板间区域内充满着匀强磁场，磁感应强度大小为B，方向垂直纸面向里，一个质量为m，带电量为+q的带电粒子自静止开始经M、N两平行金属板间的电场加速后，从A、B两板的中间沿垂直于磁感线的方向射入磁场．（不计粒子的重力）求：（1）若粒子的初速度为0，M、N两板间的电压为U，求射出电场时粒子的速度？
（2）粒子以上述速度射入匀强磁场后做圆周运动的半径是多大？
（3）MN两极板间的电压U应在什么范围内，粒子才能从磁场内射出？
分析：（1）根据动能定理求速度．
（2）粒子在磁场中做圆周运动，由洛伦兹力提供向心力，由牛顿第二定律求出半径，
（3）当粒子从平行板左边射出时，最大半径为r1=
，粒子从左边射出必须满足r≤r1．当粒子恰好从平行板右边射出时，由几何知识半径r2，即为粒子从右边射出时运动轨迹最小半径．由半径公式和动能定理求解电压的范围．
（2）粒子在磁场中做圆周运动，由洛伦兹力提供向心力，由牛顿第二定律求出半径，
（3）当粒子从平行板左边射出时，最大半径为r1=
| d |
| 4 |
解答：解：①由动能定理得：qU=
mV2
解得：v=
②进入磁场后洛伦兹力充当向心力：
qVB=m
解得：R=
③当粒子从平行板左边射出时，最大半径为r1=
，粒子从左边射出必须满足r≤r1．
即：
≥
，解得：U＜
当粒子恰好从平行板右边射出时，由几何知识知半径
r2=
r2≤R
R=
联立得：U＞
答：（1）若粒子的初速度为0，M、N两板间的电压为U，射出电场时粒子的速度v=
（2）粒子以上述速度射入匀强磁场后做圆周运动的半径是
（3）MN两极板间的电压
＞U＞
范围内，粒子才能从磁场内射出．
| 1 |
| 2 |
解得：v=
|
②进入磁场后洛伦兹力充当向心力：
qVB=m
| V2 |
| R |
解得：R=
| 1 |
| B |
|
③当粒子从平行板左边射出时，最大半径为r1=
| d |
| 4 |
即：
| d |
| 4 |
| 1 |
| B |
|
| qB2d2 |
| 32m |
当粒子恰好从平行板右边射出时，由几何知识知半径
r2=
| L2+(r2-d)2 |
r2≤R
R=
| 1 |
| B |
|
联立得：U＞
| qB2(d2+4l2)2 |
| 32md2 |
答：（1）若粒子的初速度为0，M、N两板间的电压为U，射出电场时粒子的速度v=
|
（2）粒子以上述速度射入匀强磁场后做圆周运动的半径是
| 1 |
| B |
|
（3）MN两极板间的电压
| qB2d2 |
| 32m |
| qB2(d2+4l2)2 |
| 32md2 |
点评：本题关键应用几何知识两种临界情况情况下，粒子圆周运动的半径，这是粒子在磁场中匀速圆周运动问题常用的方法．
练习册系列答案
相关题目
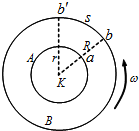1920年科学家史特恩测定气体分子速率的装置如图所示，A、B为一双层共轴圆筒形容器，外筒半径为R，内筒半径为r，可同时绕其共同轴以同一角速度ω高速旋转，其内部抽成真空．沿共同轴装有一根镀银的铂丝K，在铂丝上通电使其加热，银分子（即原子）蒸发成气体，其中一部分分子穿过A筒的狭缝a射出到达B筒的内表面．由于分子由内筒到达外筒需要一定时间，若容器不动，这些分子将到达外筒内壁上的b点，若容器转动，从a穿过的这些分子仍将沿原来的运动方向到达外筒内壁，但容器静止时的b点已转过弧长s到达b’点．
如图所示，a、b为一根方向竖直向上的电场线上的两点，一带电质点在点a由静止释放，沿电场线向上运动，到点b速度恰好为零，下列说法正确的是（ ）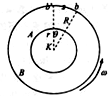
1920年科学家斯特恩测定气体分子速率的装置如图所示，A、B为一双层共轴圆筒形容器，外筒半径为R内筒半径为r，可同时绕其几何轴经同一角速度ω高速旋转，其内部抽成真空．沿几何轴装有一根镀银的铂丝K，在铂丝上通电使其加热，银分子（即原子）蒸发成气体，其中一部分分子穿过A筒的狭缝a射出到达B筒的内表面．由于分子由内筒到达外筒需要一定时间．若容器不动，这些分子将到达外筒内壁上的b点，若容器转动，从a穿过的这些分子仍将沿原来的运动方向到达外筒内壁，但容器静止时的b点已转过弧长s到达b’点．（1）这个实验运用了