题目内容
如图所示，在xoy区域内的第Ⅰ象限内有磁感应强度为B的匀强磁场，方向垂直xoy平面向外，区域内的其他象限无磁场．在A（L，0）点有一电子以速度v沿y轴正方向射入磁场．求电子在磁场中的运动时间．
【答案】分析：根据洛伦兹力提供向心力，由牛顿第二定律与几何关系，可求出初速度；从而根据电子速度与初速度的大小相比，进而确定在磁场中运动的时间．
解答：
解：设电子以v的速度射入磁场时，刚好从原点O离开磁场（如图），
这时电子在磁场中的运动半径为：
又
得：
（1）当电子速度
时，其运动半径小于或等于
，电子将从x轴上的某点离开磁场，运动时间为半个周期，
（2）当电子速度
时，其运动半径大于
，电子将从y轴上某点（如D点）离开磁场．
设此时的圆心为O′，由图可知，
所以：
答：电子在磁场中的运动时间
或
．
点评：考查牛顿第二定律的应用，掌握电子在磁场中运动时间与周期公式及圆心角有关，并会画出正确的运动轨迹图．
解答：
解：设电子以v的速度射入磁场时，刚好从原点O离开磁场（如图），这时电子在磁场中的运动半径为：
又
得：
（1）当电子速度
时，其运动半径小于或等于，电子将从x轴上的某点离开磁场，运动时间为半个周期，（2）当电子速度
时，其运动半径大于，电子将从y轴上某点（如D点）离开磁场．设此时的圆心为O′，由图可知，
所以：
答：电子在磁场中的运动时间
或．点评：考查牛顿第二定律的应用，掌握电子在磁场中运动时间与周期公式及圆心角有关，并会画出正确的运动轨迹图．
练习册系列答案
相关题目
如图所示，在xOy平面的第一象限内存在着方向垂直纸面向外，磁感应强度为B的匀强磁场，在第四象限内存在方向沿负x方向的匀强电场．从y轴上坐标为（0，a）的P点同时沿垂直磁场方向向磁场区发射速度大小不是都相等的带正电的同种粒子，粒子的速度方向在与y轴正方向成30°～150°角的范围内，结果所有粒子经过磁场偏转后都垂直打到x轴上，然后进入第四象限内的电场区．已知带电粒子电量为+q，质量为m，不计粒子重力和粒子间的相互作用力．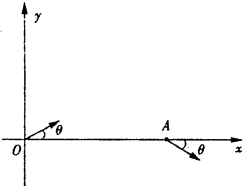
如图所示，在xOy平面内，一质量为m，电荷量为q的带电粒子（重力不计）以速度v0从坐标原点O沿与+x方向成θ角射人第一象限区，并从x轴上A的点离开第一象限区．
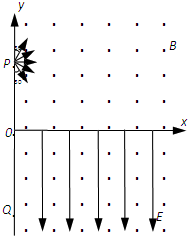如图所示，在 xOy 平面的第一、四象限内存在着方向垂直纸面向外，磁感应强度为 B 的匀强磁场，在第四象限内存在方向沿-y 方向、电场强度为 E 的匀强电场．从 y 轴上坐标为（0，a）的 P 点向磁场区发射速度大小不等的带正电同种粒子，速度方向范围是与+y 方向成30°-150°角，且在 xOy 平面内．结果所有粒子经过磁场偏转后都垂直打到 x 轴上，然后进入第四象限内的正交电磁场区．已知带电粒子电量为+q，质量为 m，粒子重力不计．
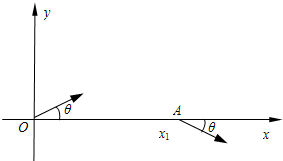如图所示，在xOy平面内，一质量为m、电荷量为+q的粒子（重力不计）以速度v0从坐标原点O沿与+x方向成θ角射入第一象限区，并从x轴上x1=a的A点离开第一象限区，速度方向与+x方向也成θ角．