��Ŀ����
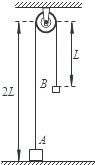 ��ͼ��ʾ��A��B����С���壨�ɿ����ʵ㣩�������ֱ�Ϊ2m��m������˨���ڿ�������ֵ�ϸ�����ˣ�ϸ�������쳤�����ܳ����㹻���������B���������ž�ֹʱ��AҲ��ֹ�ڵ����ϣ�A��B�붨��������֮�����ֱ����ֱ�Ϊ2L��L���ֽ�B������ֱ������߾���l���ٽ���Ӿ�ֹ�ͷţ�ÿ��ϸ������ֱʱA��B�ٶȵĴ�С���������ȣ����ٶȷ����෴������ϸ������ֱ��ʱ�伫�̣��˹��������������ÿ��Ժ��Բ��ƣ����������Ӵ�ʱ���ٶ�������Ϊ0��ֱ���ٴα�ϸ������ϸ��ʼ���ڻ����ϣ��Ҳ���һ��Ħ�����������ٶ�Ϊg����
��ͼ��ʾ��A��B����С���壨�ɿ����ʵ㣩�������ֱ�Ϊ2m��m������˨���ڿ�������ֵ�ϸ�����ˣ�ϸ�������쳤�����ܳ����㹻���������B���������ž�ֹʱ��AҲ��ֹ�ڵ����ϣ�A��B�붨��������֮�����ֱ����ֱ�Ϊ2L��L���ֽ�B������ֱ������߾���l���ٽ���Ӿ�ֹ�ͷţ�ÿ��ϸ������ֱʱA��B�ٶȵĴ�С���������ȣ����ٶȷ����෴������ϸ������ֱ��ʱ�伫�̣��˹��������������ÿ��Ժ��Բ��ƣ����������Ӵ�ʱ���ٶ�������Ϊ0��ֱ���ٴα�ϸ������ϸ��ʼ���ڻ����ϣ��Ҳ���һ��Ħ�����������ٶ�Ϊg������1��ϸ����һ�α���ֱ˲������A�����Ĵ�С��
��2��A��һ���������̾����������߶ȣ�
��3��A�˶�����·�̣�
��������1���������������˶��Ĺ��ɿ�������½��߶�Ϊlʱ���ٶȣ��ٸ��ݶ�������������ö�A�ij����Ĵ�С��
��2������A��B��ɵ�ϵͳ��е���غ㣬�������A���������ĸ߶ȣ�
��3������AB֮��ÿ�ε�����ã��ҳ�����õĹ��ɣ��ܽ���ɿ������A�˶�����·�̣�
��2������A��B��ɵ�ϵͳ��е���غ㣬�������A���������ĸ߶ȣ�
��3������AB֮��ÿ�ε�����ã��ҳ�����õĹ��ɣ��ܽ���ɿ������A�˶�����·�̣�
����⣺
��1��B���������壬�½��߶�Ϊlʱ���ٶ�Ϊv0������vt2-v02=2ax��v0=
��ʱϸ������ֱ��A��B�ٶȵĴ�С�������v1�������Ӷ�A��B�ij�����СΪI�����ݶ��������ö�B��-I=mv1-mv0��A��I=2mv1���ϸ����һ�α���ֱ˲������A�����Ĵ�СI=
��2���ɣ�1���ɵ�A��һ���뿪����ʱ�ٶȵĴ�Сv1=
=
��A�뿪���浽A�ٴλص�����Ĺ����У�A��B��ɵ�ϵͳ��е���غ㣬����A��һ���������̾����������߶�Ϊx1����
(m+2m)
+mgl=2mgx1+mg(l-x1)��� x1=
=
��3����A�뿪���浽A�ٴλص�����Ĺ����У�A��B��ɵ�ϵͳ��е���غ㣬���ԣ�A�ٴλص�����ʱ�ٶȵĴ�С��ȻΪv1����B�ٴλص��������߶�Ϊlʱ�ٶȵĴ�СҲΪv1���˺�B����ֱ�����˶�����ؾ������߶�Ϊlʱ�ٶȵĴ�С����v1��
���ݣ�1�����ɵ�A�ڶ����뿪����ʱ�ٶȵĴ�Сv2=
ͬ������A�ڶ����뿪�������������߶�Ϊx2=
=
?
��
A��n���뿪����ʱ�ٶȵĴ�Сvn=
=
ͬ������A��n���뿪�������������߶�Ϊxn=
=
?
����A����������B��������A���ջᾲֹ�ڵ����ϣ�
����A�˶�����·��x=2��x1+x2+��+xn+����=
(1+
+��+
+��)=
l��
��1��B���������壬�½��߶�Ϊlʱ���ٶ�Ϊv0������vt2-v02=2ax��v0=
| 2gl |
��ʱϸ������ֱ��A��B�ٶȵĴ�С�������v1�������Ӷ�A��B�ij�����СΪI�����ݶ��������ö�B��-I=mv1-mv0��A��I=2mv1���ϸ����һ�α���ֱ˲������A�����Ĵ�СI=
2m
| ||
| 3 |
��2���ɣ�1���ɵ�A��һ���뿪����ʱ�ٶȵĴ�Сv1=
| v0 |
| 3 |
| ||
| 3 |
��A�뿪���浽A�ٴλص�����Ĺ����У�A��B��ɵ�ϵͳ��е���غ㣬����A��һ���������̾����������߶�Ϊx1����
| 1 |
| 2 |
| v | 2 1 |
3
| ||
| 2g |
| l |
| 3 |
��3����A�뿪���浽A�ٴλص�����Ĺ����У�A��B��ɵ�ϵͳ��е���غ㣬���ԣ�A�ٴλص�����ʱ�ٶȵĴ�С��ȻΪv1����B�ٴλص��������߶�Ϊlʱ�ٶȵĴ�СҲΪv1���˺�B����ֱ�����˶�����ؾ������߶�Ϊlʱ�ٶȵĴ�С����v1��
���ݣ�1�����ɵ�A�ڶ����뿪����ʱ�ٶȵĴ�Сv2=
| v1 |
| 3 |
ͬ������A�ڶ����뿪�������������߶�Ϊx2=
3
| ||
| 2g |
| 1 |
| 32 |
3
| ||
| 2g |
��
A��n���뿪����ʱ�ٶȵĴ�Сvn=
| vn-1 |
| 3 |
| v1 |
| 3n-1 |
ͬ������A��n���뿪�������������߶�Ϊxn=
3
| ||
| 2g |
| 1 |
| 32(n-1) |
3
| ||
| 2g |
����A����������B��������A���ջᾲֹ�ڵ����ϣ�
����A�˶�����·��x=2��x1+x2+��+xn+����=
3
| ||
| g |
| 1 |
| 32 |
| 1 |
| 32(n-1) |
| 3 |
| 4 |
����������AB֮��ĵ�һ�ε�����ã������ܽ�֮���ÿ������õĹ��ɣ�����AB����õĹ���������⣬�ҳ������ǽ������Ĺؼ���

��ϰ��ϵ�д�
 �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�����Ŀ
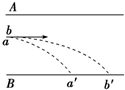 ��ͼ��ʾ��a��b��������������ӣ�����ͬ���ٶ��Ⱥ�ֱ�ڵ糡�ߴ�ͬһ�����ƽ�а�����ǿ�糡��a���Ӵ���B���a��㣬b���Ӵ���B���b��㣬������������������
��ͼ��ʾ��a��b��������������ӣ�����ͬ���ٶ��Ⱥ�ֱ�ڵ糡�ߴ�ͬһ�����ƽ�а�����ǿ�糡��a���Ӵ���B���a��㣬b���Ӵ���B���b��㣬������������������| A��a�ĵ����һ������b�ĵ���� | B��b������һ������a������ | C��a�ıȺ�һ������b�ıȺ� | D��b�ıȺ�һ������a�ıȺ� |
 ��ͼ��ʾ��A��B�������������ֱ���GA=3N��GB=4N�����ɵ��������ƣ�����װ������ֱ�����ھ�ֹ״̬����ʱ���ɵĵ���F=2N�����컨���ܵ��������͵ذ��ܵ���ѹ�����п����ǣ�������
��ͼ��ʾ��A��B�������������ֱ���GA=3N��GB=4N�����ɵ��������ƣ�����װ������ֱ�����ھ�ֹ״̬����ʱ���ɵĵ���F=2N�����컨���ܵ��������͵ذ��ܵ���ѹ�����п����ǣ������� ��ͼ��ʾ��A��B������������������Ϊ100N������������mA=4kg��mB=8kg��������F�����������ϼ����˶���Ϊʹ�����������ϣ�F�����ֵ�Ƕ��٣���gȡ10m/s2��
��ͼ��ʾ��A��B������������������Ϊ100N������������mA=4kg��mB=8kg��������F�����������ϼ����˶���Ϊʹ�����������ϣ�F�����ֵ�Ƕ��٣���gȡ10m/s2��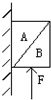 ��ͼ��ʾ��A��B�������屻һ����ֱ������F���ţ����ھ�ֹ״̬����A����һ����
��ͼ��ʾ��A��B�������屻һ����ֱ������F���ţ����ھ�ֹ״̬����A����һ����