题目内容
 (2011?湖州模拟)如图所示,竖直平面内有一与水平面成θ=30°的绝缘斜面轨道AB,该轨道和一半径为R的光滑绝缘圆弧轨道BCD相切于B点.整个轨道处于竖直向下的匀强电场中,现将一质量为m带正电的滑块(可视为质点)从斜面上的A点静止释放,滑块能沿轨道运动到圆轨道的最高D点后恰好落到斜面上与圆心O等高的P点,已知带电滑块受到的电场力大小为Eq=mg,滑块与斜面轨道间的动摩擦因数为μ=
(2011?湖州模拟)如图所示,竖直平面内有一与水平面成θ=30°的绝缘斜面轨道AB,该轨道和一半径为R的光滑绝缘圆弧轨道BCD相切于B点.整个轨道处于竖直向下的匀强电场中,现将一质量为m带正电的滑块(可视为质点)从斜面上的A点静止释放,滑块能沿轨道运动到圆轨道的最高D点后恰好落到斜面上与圆心O等高的P点,已知带电滑块受到的电场力大小为Eq=mg,滑块与斜面轨道间的动摩擦因数为μ=
| ||
| 6 |
(1)滑块经过D点时的速度大小;
(2)滑块经过圆轨道最低C点时,轨道对滑块的支持力FC;
(3)B处的速度及A、B两点之间的距离d.
分析:(1)滑块离开D点后做类平抛运动,分解为水平方向和竖直方向,水平方向做匀速直线运动,竖直方向做初速度为0的匀加速直线运动,根据牛顿第二定律,求出竖直方向上的加速度,然后求出时间,再根据水平方向上的匀速直线运动求出初速度.
(2)对C到D过程运用动能定理,求出C点的速度,在C点受到重力,支持力,电场力,三个力的合力提供向心力,从而求出支持力.
(3)对B到C运用动能定理求出B点的速度,再对A到B的过程运用动能定理,求出AB间的距离.
(2)对C到D过程运用动能定理,求出C点的速度,在C点受到重力,支持力,电场力,三个力的合力提供向心力,从而求出支持力.
(3)对B到C运用动能定理求出B点的速度,再对A到B的过程运用动能定理,求出AB间的距离.
解答:解:(1)滑块从D到P过程中做类平抛运动:Eq+mg=ma
得:a=2g
=vDt
R=
2gt2
得:vD=2
(2)滑块 C→D:根据动能定理
m
-
m
=-mg?2R-Eq?2R
得:vC=2
FC-mg-Eq=m
得:FC=14mg
(3)B→C:
m
-
m
=(mg+Eq)(R-Rcos300)
得:vB=
滑块A→B:根据动能定理-μ(Eq+mg)cos300?d+(Eq+mg)?dsin300=
m
得:d=(8+2
)R.
得:a=2g
| R |
| sin300 |
R=
| 1 |
| 2 |
得:vD=2
| gR |
(2)滑块 C→D:根据动能定理
| 1 |
| 2 |
| v | 2 D |
| 1 |
| 2 |
| v | 2 C |
得:vC=2
| 3gR |
FC-mg-Eq=m
| ||
| R |
得:FC=14mg
(3)B→C:
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |
得:vB=
| gd |
滑块A→B:根据动能定理-μ(Eq+mg)cos300?d+(Eq+mg)?dsin300=
| 1 |
| 2 |
| v | 2 B |
得:d=(8+2
| 3 |
点评:解决本题的关键是合力地选择研究的过程然后运用动能定理求解.以及知道在圆周运动的最低点,合力提供圆周运动的向心力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011?湖州模拟)如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.滑杆MN垂直于导轨并可在导轨上滑动.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一质量为m的物块相连,绳处于拉直状态.现若从静止开始释放物块,用i表示回路中的感应电流,g表示重力加速度,则在物块下落过程中物块的速度可能( )
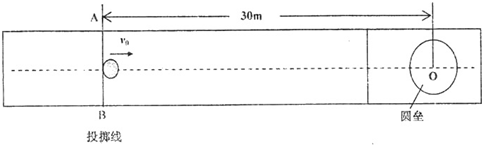
(2011?湖州模拟)如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.滑杆MN垂直于导轨并可在导轨上滑动.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一质量为m的物块相连,绳处于拉直状态.现若从静止开始释放物块,用i表示回路中的感应电流,g表示重力加速度,则在物块下落过程中物块的速度可能( )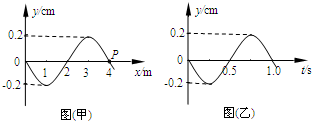 (2011?湖州模拟)一列横波在x轴上传播,图(甲)为t=0.5s时的波动图象,图(乙)为介质中质点P的振动图象.对该波的传播方向和传播波速度的说法正确的是( )
(2011?湖州模拟)一列横波在x轴上传播,图(甲)为t=0.5s时的波动图象,图(乙)为介质中质点P的振动图象.对该波的传播方向和传播波速度的说法正确的是( ) (2011?湖州模拟)如图所示匀强电场E的区域内,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心、半径为R的球面上的点,o、a、e、c、f点共面且与电场平行,o、b、e、d、f点共面且与电场垂直,则下列说法中正确的是( )
(2011?湖州模拟)如图所示匀强电场E的区域内,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心、半径为R的球面上的点,o、a、e、c、f点共面且与电场平行,o、b、e、d、f点共面且与电场垂直,则下列说法中正确的是( )