题目内容
由内壁光滑的细管制成的直角三角形管道ABC安放在竖直平面内，BC边水平，AC管长5m，直角C处是小的圆弧，∠B=37º。从角A处无初速度地释放两个光滑小球（小球的直径比管径略小），第一个小球沿斜管AB到达B处，第二个小球沿竖管AC到C再沿横管CB到B处，（已知
，管内无空气阻力，取g=10m/s2）求
(1) 两小球到达B点时的速度大小之比
(2) 两小球到达B点时的时间之比
【答案】
（1）
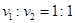
（2）
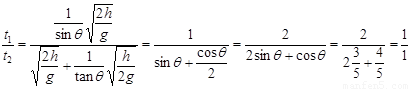
【解析】（17分）（1）设AC长为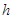
，小球到达B点时的速度为
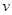，根据机械能守恒定律，
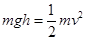……………（3分）
所以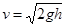
……………（2分）
可见小球的速度只与高度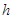有关，与路径无关，
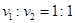……………（3分）
（2） 第一个小球的运动时间由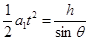
定 ……（1分）
根据牛顿第二定律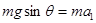
得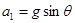
……（1分）
故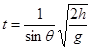
……（1分）
第二个小球在竖管中的运动时间由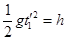
得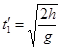
……………⑤（2分）
第二个小球在横管中做匀速直线运动，运动时间由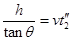
定…………（1分）
所以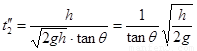
…………（2分）
所求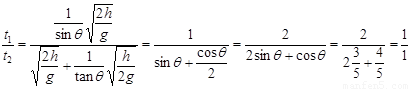…………（2分）
***该比值与h及g的取值无关
练习册系列答案
阅读快车系列答案
相关题目
如图所示，AB是根据某平抛运动轨迹制成的内壁光滑的细圆管轨道，轨道上端A与一光滑斜槽的末端水平面相切．已知细圆管轨道的水平长度为S=2.4m；两端口连线与水平方向的夹角α=37°．（取sin37°=0.6，cos37°=0.8，g=10m/s2）求