题目内容
质量为800kg的小汽车驶过一半径为40m的圆形拱桥,到达桥顶时速度为5m/s,求此时汽车对桥面的压力是
7500
7500
N;若要使汽车到达桥顶不脱离桥面,则汽车的最大速度是20
20
m/s.分析:(1)汽车经过拱桥最高点时,由重力和桥面的支持力的合力提供向心力,根据向心力公式和牛顿第二、第三定律可列式求解;
(2)若要使汽车到达桥顶不脱离桥面,汽车对桥恰好无压力,重力完全提供汽车的向心力,根据向心力公式和牛顿第二定律可列式求解.
(2)若要使汽车到达桥顶不脱离桥面,汽车对桥恰好无压力,重力完全提供汽车的向心力,根据向心力公式和牛顿第二定律可列式求解.
解答:解:(1)如图所示,汽车到达桥顶时,竖直方向受到重力G和桥对它的支持力N的作用.
汽车对桥顶的压力大小等于桥顶对汽车的支持力N,汽车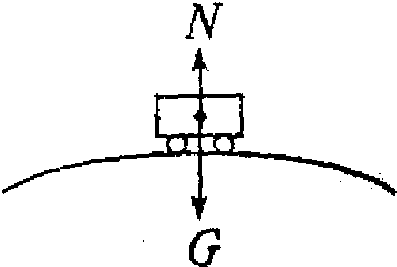 过桥时做圆周运动,重力和支持力的合力提供向心力,根据牛顿第二定律得:
过桥时做圆周运动,重力和支持力的合力提供向心力,根据牛顿第二定律得:
G-N=m
有:N=G-F=mg-m
=8000N-800×
N=7500N,
根据牛顿第三定律可知,此时汽车对桥的压力大小为:N′=N=7500N,方向竖直向下
(2)若要使汽车到达桥顶不脱离桥面,汽车经过桥顶恰好对桥没有压力,则N=0,即汽车做圆周运动的向心力完全由其自身重力来提供,所以有:
mg=m
解得:v=
=
m/s=20m/s
即要使汽车到达桥顶不脱离桥面,汽车的最大速度是20m/s.
故答案为:7500,20
汽车对桥顶的压力大小等于桥顶对汽车的支持力N,汽车
 过桥时做圆周运动,重力和支持力的合力提供向心力,根据牛顿第二定律得:
过桥时做圆周运动,重力和支持力的合力提供向心力,根据牛顿第二定律得:G-N=m
| v2 |
| R |
有:N=G-F=mg-m
| v2 |
| R |
| 52 |
| 40 |
根据牛顿第三定律可知,此时汽车对桥的压力大小为:N′=N=7500N,方向竖直向下
(2)若要使汽车到达桥顶不脱离桥面,汽车经过桥顶恰好对桥没有压力,则N=0,即汽车做圆周运动的向心力完全由其自身重力来提供,所以有:
mg=m
| ||
| R |
解得:v=
| gR |
| 10×40 |
即要使汽车到达桥顶不脱离桥面,汽车的最大速度是20m/s.
故答案为:7500,20
点评:本题关键找出车经过桥的最高点时的向心力来源,然后根据牛顿第二定律和向心力公式列式进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目