题目内容
8.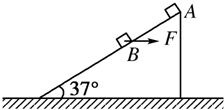 如图所示,有一足够长的斜面,倾角α=37°.一质量为m=1kg的小物块从斜面顶端A处静止下滑,到B处后,受一水平向右的恒力F作用,小物块最终停在C点(C点未画出).若AB长为2.25m,BC长为0.5m.小物块与斜面间动摩擦因数μ=0.5,sin 37°=0.6,cos 37°=0.8,g=10m/s2.求:
如图所示,有一足够长的斜面,倾角α=37°.一质量为m=1kg的小物块从斜面顶端A处静止下滑,到B处后,受一水平向右的恒力F作用,小物块最终停在C点(C点未画出).若AB长为2.25m,BC长为0.5m.小物块与斜面间动摩擦因数μ=0.5,sin 37°=0.6,cos 37°=0.8,g=10m/s2.求:(1)小物块到达B点的速度多大;
(2)水平恒力F的大小.
分析 (1)根据牛顿第二定律可求得加速度,再根据速度位移公式可求得到达B点时的速度;
(2)对两过程分析,明确第一过程的末速度等于后一段的初速度,根据速度和位移关系即可求得第二段的加速度,再根据牛顿第二定律可求得拉力大小.
解答 解:(1)设小物块在AB段的加速度为a1,有
mgsin 37°-μmgcos 37°=ma1 ①
代入数据解得a1=2 m/s2 ②
到达B点的速度vB=$\sqrt{2{a}_{1}{x}_{1}}$═$\sqrt{2×2×2.25}$ m/s=3 m/s.
(2)设小物块在BC段的加速度大小为a2,
有 vB2=2a1xAB=2a2xBC ③
得 a2=9 m/s2
此阶段对物块受力分析:
Fcos 37°+μFN-mgsin 37°=ma2 ④
FN=Fsin 37°+mgcos 37° ⑤
联立得F=10N
答:(1)小物块到达B点的速度为3m/s;
(2)水平恒力F的大小为10N.
点评 本题考查牛顿第二定律的应用,要注意正确分析物理过程,对每一过程做好受力分析,才能根据牛顿第二定律准确求解,同时注意两过程中的速度关系.

练习册系列答案
相关题目
19.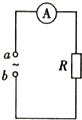 如图所示,电路中电阻的阻值R=100Ω,电流表为理想电流表,在a、b之间接入电压U=220$\sqrt{2}$sin100πt(V)的交流电源,则( )
如图所示,电路中电阻的阻值R=100Ω,电流表为理想电流表,在a、b之间接入电压U=220$\sqrt{2}$sin100πt(V)的交流电源,则( )
 如图所示,电路中电阻的阻值R=100Ω,电流表为理想电流表,在a、b之间接入电压U=220$\sqrt{2}$sin100πt(V)的交流电源,则( )
如图所示,电路中电阻的阻值R=100Ω,电流表为理想电流表,在a、b之间接入电压U=220$\sqrt{2}$sin100πt(V)的交流电源,则( )| A. | 电流表的示数为2.2 A | |
| B. | t=0.01s时,电流表的示数为零 | |
| C. | 若产生该交流电的发电机的线框转速提高一倍,其他条件不变,则电流表的示数也增大一倍 | |
| D. | 若将电阻换成200Ω,则电源的输出功率变为原来的两倍 |
16.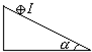 如图所示,在匀强磁场B的区域中有一光滑斜面体,在斜面上放了一根长L,质量为m的导线,当通以如图示方向的电流I后,导线恰能保持静止,则磁感应强度B必须满足( )
如图所示,在匀强磁场B的区域中有一光滑斜面体,在斜面上放了一根长L,质量为m的导线,当通以如图示方向的电流I后,导线恰能保持静止,则磁感应强度B必须满足( )
 如图所示,在匀强磁场B的区域中有一光滑斜面体,在斜面上放了一根长L,质量为m的导线,当通以如图示方向的电流I后,导线恰能保持静止,则磁感应强度B必须满足( )
如图所示,在匀强磁场B的区域中有一光滑斜面体,在斜面上放了一根长L,质量为m的导线,当通以如图示方向的电流I后,导线恰能保持静止,则磁感应强度B必须满足( )| A. | B=$\frac{mgtanα}{IL}$,方向竖直向上 | B. | B=$\frac{mg}{IL}$,方向水平向左 | ||
| C. | B=$\frac{mg•sinα}{IL}$,方向垂直斜面向上 | D. | B=$\frac{mg•sinα}{IL}$,方向垂直斜面向下 |

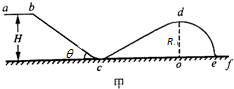 滑板运动是一项陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作给人以美的享受.如图甲所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=37°,de段是一半径R=2.5m的四分之一圆弧轨道,O点为圆心,其正上方的d点为圆弧的最高点,滑板及运动员总质量m=60kg,运动员滑经d点时轨道对滑板支持力用Nd表示,忽略摩擦阻力和空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.除下述问(2)中运动员做缓冲动作以外,均可把滑板及运动员视为质点.
滑板运动是一项陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作给人以美的享受.如图甲所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=37°,de段是一半径R=2.5m的四分之一圆弧轨道,O点为圆心,其正上方的d点为圆弧的最高点,滑板及运动员总质量m=60kg,运动员滑经d点时轨道对滑板支持力用Nd表示,忽略摩擦阻力和空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.除下述问(2)中运动员做缓冲动作以外,均可把滑板及运动员视为质点. 如图所示,R为电阻箱,V为理想电压表,当电阻箱读数为R1=2Ω时,电压表读数为U1=4V;当电阻箱读数为R2=5Ω时,电压表读数为U2=5V.求:
如图所示,R为电阻箱,V为理想电压表,当电阻箱读数为R1=2Ω时,电压表读数为U1=4V;当电阻箱读数为R2=5Ω时,电压表读数为U2=5V.求: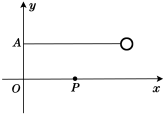 如图所示,在竖直平面内有xOy坐标系,长为l的不可伸长细绳,一端固定在A点,A点的坐标为(0、$\frac{l}{3}$),另一端系一质量为m的小球.现在x坐标轴上(x>0)固定一个小钉,拉小球使细绳绷直并呈水平位置,再让小球从静止释放,当细绳碰到钉子以后,小球可以绕钉子在竖直平面内做圆周运动.
如图所示,在竖直平面内有xOy坐标系,长为l的不可伸长细绳,一端固定在A点,A点的坐标为(0、$\frac{l}{3}$),另一端系一质量为m的小球.现在x坐标轴上(x>0)固定一个小钉,拉小球使细绳绷直并呈水平位置,再让小球从静止释放,当细绳碰到钉子以后,小球可以绕钉子在竖直平面内做圆周运动.