题目内容
质量为 10kg的物体在F=200N的水平推力作用下，从粗糙斜面的底端由静止开始沿斜面运动，斜面足够长且固定不动，与水平地面的夹角θ=37°．力F作用8秒钟后撤去，物体在斜面上继续上滑了5秒钟后，速度减为零．求：物体与斜面间的动摩擦因数μ．（已知 sin37°=0.6，cos37°=0.8，g=10m/s2）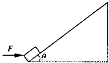
【答案】分析：物体先做匀加速直线运动，后做匀减速直线运动．根据牛顿第二定律和运动学公式结合研究匀加速运动过程，求出F刚撤去时物体的速度表达式，再由牛顿第二定律和运动学公式结合研究匀减速运动过程，联立可求出μ．
解答：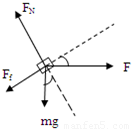
解：对于匀加速直线运动过程：
物体的受力情况如图，根据牛顿第二定律得：
Fcosθ-Ff-mgsinθ=ma1 ①
又Ff=μFN=μ（Fsinθ+mgcosθ） ②
F刚撤去时物体的速度为v=a1t1 ③
联立①②③得：[Fcosθ-μ（Fsinθ+mgcosθ）-mgsinθ]t1=mv ④
对于匀减速直线运动过程：
-Ff-mgsinθ=ma2 ⑤
0=v+a2t2 ⑥
联立②⑤⑥得：
[-μmgcosθ-mgsinθ]t2=-mv ⑦
联立④⑦得：：[Fcosθ-μ（Fsinθ+mgcosθ）-mgsinθ]t1=（μmgcosθ+mgsinθ）t2⑧
代入数据解得μ=0.25
答：物体与斜面间的动摩擦因数μ为0.25．
点评：本题是两个过程的动力学问题，运用牛顿第二定律和速度公式结合分别研究两个过程，求出动摩擦因数μ，关键要正确分析受力情况，求出加速度．
解答：
解：对于匀加速直线运动过程：物体的受力情况如图，根据牛顿第二定律得：
Fcosθ-Ff-mgsinθ=ma1 ①
又Ff=μFN=μ（Fsinθ+mgcosθ） ②
F刚撤去时物体的速度为v=a1t1 ③
联立①②③得：[Fcosθ-μ（Fsinθ+mgcosθ）-mgsinθ]t1=mv ④
对于匀减速直线运动过程：
-Ff-mgsinθ=ma2 ⑤
0=v+a2t2 ⑥
联立②⑤⑥得：
[-μmgcosθ-mgsinθ]t2=-mv ⑦
联立④⑦得：：[Fcosθ-μ（Fsinθ+mgcosθ）-mgsinθ]t1=（μmgcosθ+mgsinθ）t2⑧
代入数据解得μ=0.25
答：物体与斜面间的动摩擦因数μ为0.25．
点评：本题是两个过程的动力学问题，运用牛顿第二定律和速度公式结合分别研究两个过程，求出动摩擦因数μ，关键要正确分析受力情况，求出加速度．
练习册系列答案
名校课堂系列答案
相关题目
质量为10kg的物块在F=200N与斜面平行的力作用下，从粗糙斜面的底端由静止开始沿斜面向上运动，斜面固定不动且足够长，斜面与水平地面的夹角θ=37°．力F作用2s后撤去，物体在斜面上继续上滑了3s后，速度减为零．已知sin37°=0.6，cos37°=0.8，g取10m/s2，不计空气阻力，求：物体沿斜面向上运动的最大位移s．
如图所示，水平面上，质量为10kg的物块A拴在一个被水平拉伸的弹簧一端，弹簧的另一端固定在小车上，小车正在以v=2m/s的速度向左匀速运动，此时弹簧对物块的弹力大小为10N时，物块相对于小车处于静止状态，若小车突然以a=2m/s2的加速度刹车时（ ）
如图所示水平面上，质量为10kg的物块A拴在一个被水平拉伸的弹簧一端，弹簧的另一端固定在小车上，小车静止不动，弹簧对物块的弹力大小为5N时，物块处于静止状态，若小车以加速度a=1m/s2沿水平地面向右加速运动时（ ）
如图，被水平拉伸的轻弹簧右端拴在小车壁上，左端拴一质量为10kg的物块M．小车静止不动，弹簧对物块的拉力大小为5N是，物块处于静止状态．当小车的加速度a=0.5m/s2沿水平地面向右加速运动时（ ）| A、物块M相对小车向左运动 | B、物块M受到的摩擦力不变 | C、物块M受到的摩擦力为零 | D、物块M受到的拉力将增大 |