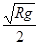Question

地球的半径为R，地面的重力加速度为g，一颗离地面高度为R的人造地球卫星绕地球做匀速圆周运动，则（　　）

• A．卫星加速度的大小为

  g

  2

• B．卫星运转的角速度为

  1

  4

  2g R

• C．卫星运转的线速度为

  1

  4

  2gR

• D．卫星运转的周期为2π

  2R g

Answer 1

分析：根据万有引力近似等于重力得出轨道上的重力加速度与轨道半径的定量关系．再结合万有引力提供向心力进行求解．

解答：解：根据万有引力等于重力得，

GMm

R2

=mg，
则GM=gR²．
根据万有引力提供向心力得，

GMm

(2R)2

=m（2R）ω²=

mv2

2R

=

m?4π2×2R

T2

=ma．
解得a=

1

4

g，
ω=

1

4

2g R

，
v=

gR 2

，
T=4π

2R g

．故B正确，A、C、D错误．
故选：B．

点评：解决本题的关键是万有引力提供向心力和万有引力近似等于重力这两知识点的综合应用，还要注意轨道半径和高度是两个不同的概念