题目内容
如图所示，A、B、C三个物块放在水平的圆盘上，它们的质量关系是mA=2mB=2mC，它们与转轴的距离的关系是2rA=2rB=rC，三个物块与圆盘表面的动摩擦因数都为μ，且它们与圆盘间的最大静摩擦力与滑动摩擦力相等，当圆盘转动时，A、B、C都没有滑动，则下列判断正确的是（ ）分析：抓住角速度相等，根据向心加速度的公式比较向心加速度的大小，通过摩擦力提供向心力比较静摩擦力的大小．根据牛顿第二定律求出临界角速度与半径的关系，判断哪个物块先滑动．
解答：解：A、三个物块做圆周运动的角速度ω相同，向心加速度a=ω2r，C离转轴最远，向心加速度最大．故A正确．
B、三个物块做圆周运动的向心力由静摩擦力Ff提供，Ff=mω2r，B与A相比，r相同，m小；B与C相比，m相同，r小，所以B的摩擦力最小．故B正确．
C、当圆盘转速增大时，物块将要滑动，静摩擦力达到最大值，最大静摩擦力提供向心力，μmg=mω2r，即ω=
，与质量无关，由于2rA=2rB=rC，B与A同时开始滑动，C比B先滑动．故C错误，D正确．
故选ABD．
B、三个物块做圆周运动的向心力由静摩擦力Ff提供，Ff=mω2r，B与A相比，r相同，m小；B与C相比，m相同，r小，所以B的摩擦力最小．故B正确．
C、当圆盘转速增大时，物块将要滑动，静摩擦力达到最大值，最大静摩擦力提供向心力，μmg=mω2r，即ω=
|
故选ABD．
点评：解决本题的关键知道物块做圆周运动的向心力来源，结合牛顿第二定律进行求解．
练习册系列答案
相关题目
如图所示，a、b、c为电场中同一电场线上的三点，且b为ac的中点，a、c电势分别为φa=8V，φc=6V．下列叙述正确的是（ ）
如图所示，A、B、C、D是某匀强电场中的4个等势面，一个质子和一个α粒子（电荷量是质子的2倍，质量是质子的4倍）同时在A等势面从静止出发，向右运动，当到达D等势面时，下列说法正确的是（ ）
如图所示，a、b和c都是厚度均匀的平玻璃板，a和b、b和c之间的夹角都为α，一细光束由红光和蓝光组成，以入射角θ从O点射入a板，且射出c板后的两束单色光通过空气射在地面上P、Q两点，由此可知（ ）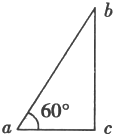
如图所示，a、b、c是匀强电场中的直角三角形的三个顶点．已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V，