Question

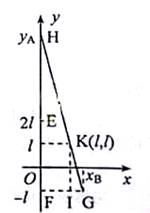
水平桌面上有两个玩具车A和B，两者用一轻质细橡皮筋相连，在橡皮筋上有一红色标记R.在初始时橡皮筋处于拉直状态，A、B和R分别位于直角坐标系中的(0，2L)、(0，－L)和(0，0)点．已知A从静止开始沿y轴正向做加速度大小为a的匀加速运动；B平行于x轴朝x轴正向匀速运动．在两车此后运动的过程中，标记R在某时刻通过点(L，L)．假定橡皮筋的伸长是均匀的，求B运动速度的大小．

Answer 1

设B车的速度大小为v.如图，标记R在时刻t通过点K(l，l)，此时A、B的位置分别为H、G.由运动学公式，H的纵坐标yA、G的横坐标xB分别为

yA＝2l＋at2①（3分）

xB＝vt②（1分）

在开始运动时，R到A和B的距离之比为2∶1，即OE∶OF＝2∶1（2分）

由于橡皮筋的伸长是均匀的，在以后任一时刻R到A和B的距离之比都为2∶1.因此，在时刻t有HK∶KG＝2∶1③

由于△FGH～△IGK，有HG∶KG＝xB∶(xB－l)④

HG∶KG＝(yA＋l)∶(2l)⑤（2分）

由③④⑤式得xB＝l⑥，yA＝5l⑦

联立①②⑥⑦式得　　v＝⑧（2分）