题目内容
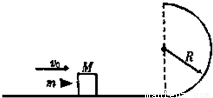 如图所示,光滑半圆轨道竖直放置,其半径为R=0.10m,一水平轨道与圆轨道相切,在水平光滑轨道上停放着一个质量为M=480g的木块,一颗质量为m=20g的子弹,以vo=100m/s的水平速度射入木块中,然后随木块一起运动到轨道最高点后水平抛出,(g取10m/s2)求:
如图所示,光滑半圆轨道竖直放置,其半径为R=0.10m,一水平轨道与圆轨道相切,在水平光滑轨道上停放着一个质量为M=480g的木块,一颗质量为m=20g的子弹,以vo=100m/s的水平速度射入木块中,然后随木块一起运动到轨道最高点后水平抛出,(g取10m/s2)求:(1)子弹射入木块之后的共同速度v;
(2)物块到达最高点时对轨道压力的大小N;
(3)当圆轨道半径R为多大时,平抛的水平距离最大.并求出平抛运动水平距离的最大值X.
【答案】分析:对子弹和木块应用动量守恒定律求出共同速度,对子弹、木块由水平轨道到最高点应用机械能守恒定律,取水平面为零势能面,求出木块到最高点时的速度,根据向心力公式求出对轨道的压力,由平抛运动的基本规律表示出平抛的水平距离即可求解.
解答:解:对子弹和木块应用动量守恒定律:
mv=(m+M)v1
所以 v1=4m/s
对子弹、木块由水平轨道到最高点应用机械能守恒定律,取水平面为零势能面,设木块到最高点时的速度为v2,有
 (m+M)v2=2(m+M)gR+
(m+M)v2=2(m+M)gR+ (m+M)vt2
(m+M)vt2
N+(m+M)g=(m+M)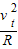
解得:N=55 (N)
根据牛顿第三定律得:在最高点根据向心力公式得:物块到达最高点时对轨道压力的大小为55N;
(3)当半径为R,时vt=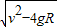
平抛时x=vt,t
2R= gt2
gt2
解得:x=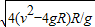 =4
=4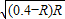
当:0.4-R=R 即:R=0.2m时,x最大
最大值x=0.8 m
答:(1)子弹射入木块之后的共同速度为4m/s;
(2)物块到达最高点时对轨道压力的大小为55N;
(3)当圆轨道半径R为0.2m时,平抛的水平距离最大.水平距离的最大值为0.8m.
点评:对于圆周运动,常常是机械能守恒定律或动能定理与牛顿定律的综合.子弹射击木块过程,基本的规律是动量守恒.
解答:解:对子弹和木块应用动量守恒定律:
mv=(m+M)v1
所以 v1=4m/s
对子弹、木块由水平轨道到最高点应用机械能守恒定律,取水平面为零势能面,设木块到最高点时的速度为v2,有
 (m+M)v2=2(m+M)gR+
(m+M)v2=2(m+M)gR+ (m+M)vt2
(m+M)vt2N+(m+M)g=(m+M)
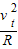
解得:N=55 (N)
根据牛顿第三定律得:在最高点根据向心力公式得:物块到达最高点时对轨道压力的大小为55N;
(3)当半径为R,时vt=
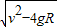
平抛时x=vt,t
2R=
 gt2
gt2解得:x=
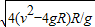 =4
=4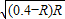
当:0.4-R=R 即:R=0.2m时,x最大
最大值x=0.8 m
答:(1)子弹射入木块之后的共同速度为4m/s;
(2)物块到达最高点时对轨道压力的大小为55N;
(3)当圆轨道半径R为0.2m时,平抛的水平距离最大.水平距离的最大值为0.8m.
点评:对于圆周运动,常常是机械能守恒定律或动能定理与牛顿定律的综合.子弹射击木块过程,基本的规律是动量守恒.

练习册系列答案
相关题目
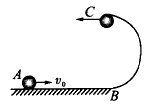
 如图所示,光滑的水平轨道与光滑半圆弧轨道相切.圆轨道半径R=0.4m,一小球停放在光滑水平轨道上,现给小球一个V0=5m/s的初速度.求:
如图所示,光滑的水平轨道与光滑半圆弧轨道相切.圆轨道半径R=0.4m,一小球停放在光滑水平轨道上,现给小球一个V0=5m/s的初速度.求: