题目内容
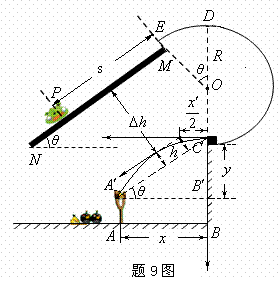
如题9图所示，弹枪
离竖直墙壁BC距离
，质量
的“愤怒的小鸟”从弹枪上
点弹出后，抛射至光滑圆弧轨道最低点C点，
的竖直高度差
。“小鸟”在C处时，速度恰好水平地与原来静止在该处的质量为
的石块发生弹性碰撞，碰后石块沿圆弧轨道上滑，圆弧轨道半径
，石块恰好能通过圆弧最高点D，之后无碰撞地从E点离开圆弧轨道进入倾斜轨道MN（无能量损失），且斜面MN的倾角
，
，石块沿斜面下滑至P点与原来藏在该处的“猪头”发生碰撞并击爆它，石块与斜面间的动摩擦因数
，PE之间的距离
。已知“小鸟”、石块、“猪头”均可视为质点，重力加速度
，空气阻力忽略不计（
，
）。求：
（1）石块与“猪头”碰撞时的速度大小；
（2）“小鸟”与石块碰前的速度大小；
（3）“小鸟”与石块相碰之前离斜面MN的最近距离。
解：
（1）石块恰好过圆弧最高点D，设在D点时的速度为
（2分）
解得
设石块在P点与“猪头”碰撞时的速度为
，石块从D至P的过程，由动能定理可知
（2分）
解得
（2分）
（2）设石块在C点碰后的速度为
，石块从C至D的过程，由动能定理可知
（2分）
解得
设“小鸟”与石块碰前的速度为v，碰后速度为
，在碰撞过程，由动量守恒和能量守恒可知
（2分）
（2分）
联解可得 
（2分）
（3）将“小鸟”从至C的运动可逆向视为从C至的平抛运动，设历时t，“小鸟”的速度与连线平行，由
（1分）
联解可得 
此时“小鸟”离连线的距离设为h
（1分）
（1分）
则“小鸟”离斜面MN最近的距离为
（1分）
得
（1分）
 |
由静止释放一个质量为m，带电量为q的正粒子，经过一段时间后，粒子从CD两极板的正中央进入电场，最后由CD两极板之间穿出电场。不计极板厚度及粒子的重力，假设装置产生的三个电场互不影响，静电力常量为k。求：
离竖直墙壁BC距离
，质量
的“愤怒的小鸟”从弹枪上
点弹出后，抛射至光滑圆弧轨道最低点C点，
的竖直高度差
。“小鸟”在C处时，速度恰好水平地与原来静止在该处的质量为
的石块发生弹性碰撞，碰后石块沿圆弧轨道上滑，圆弧轨道半径
，石块恰好能通过圆弧最高点D，之后无碰撞地从E点离开圆弧轨道进入倾斜轨道MN（无能量损失），且斜面MN的倾角
，
，石块沿斜面下滑至P点与原来藏在该处的“猪头”发生碰撞并击爆它，石块与斜面间的动摩擦因数
，PE之间的距离
。已知“小鸟”、石块、“猪头”均可视为质点，重力加速度
，空气阻力忽略不计（
，
）。求：