题目内容
3.如图甲所示,放在光滑水平地面上的长木板质量M=0.5kg,木板右端放一质量m=0.5kg的滑块(可视为质点),滑块与木板间的动摩擦因数μ=0.4;滑块的正上方有一悬点O,通过长l=0.8m的轻绳吊一质量m0=1.0kg的小球.现将小球拉至与O点处于同一水平位置,由静止释放,小球摆至最低点时与滑块发生正碰,且m0与m只碰一次,小球碰后的动能与其向上摆动高度的关系如图乙所示,g取10m/s2,求:
(1)碰前瞬间绳子对小球拉力的大小;
(2)碰后瞬间滑块速度的大小;
(3)要使滑块不会从木板上滑下,则木板的长度应滿足什么条件?
分析 1、由机械能守恒定律求得最低点速度,由牛顿第二定律求得绳子对小球拉力的大小;
2、根据小球与滑块碰撞过程动量守恒和碰撞前后的总动能关系求解;
3、当滑块和长木板共速时滑块恰好在木板的最右端,根据动量守恒和功能关系求解.
解答 解:(1)设小球摆动到最低点速度为v0,绳对小球拉力为T,由机械能守恒定律得:
${m_0}gl=\frac{1}{2}{m_0}v_0^2$
代入数据解得:v0=4m/s
由牛顿第二定律得:
$T-{m_0}g={m_0}\frac{v_0^2}{l}$
解得:$T={m_0}g+{m_0}\frac{v_0^2}{l}=30N$
(2)设碰后小球、滑块速度分别为v1和v2,
由图象可得:${E_k}={m_0}gh=\frac{1}{2}{m_0}v_1^2$
得:v1=2m/s,或$v{{\;}_1^′}=-2m/s$
规定向右为正方向,小球与滑块碰撞过程动量守恒,得:
m0v0=m0v1+mv2
代入数据解得:v2=4m/s,或$v{{\;}_2^′}=12m/s$
计算碰撞前后的总动能可知:$\frac{1}{2}{m_0}v_0^2>\frac{1}{2}{m_0}v_1^2+\frac{1}{2}mv_2^2$,合理
而 $\frac{1}{2}{m_0}v_0^2<\frac{1}{2}{m_0}v_1^{'2}+\frac{1}{2}mv_2^{'2}$,不合理
所以碰后滑块速度只能取:v2=4m/s
(3)当滑块和长木板共速时滑块恰好在木板的最右端,设板长为l1.由动量守恒得:
mv2=(m+M)v3
由功能关系得:
$μmgl=\frac{1}{2}mv_2^2-\frac{1}{2}(m+M)v{{\;}_3^2}$
联立并代入数据解得:l=1m
答:(1)碰前瞬间绳子对小球拉力的大小是30N;
(2)碰后瞬间滑块速度的大小是4m/s;
(3)要使滑块不会从木板上滑下,则木板的长度应滿足l=1m.
点评 本题考查了求拉力、木板长度问题,分析清楚物体运动过程,应用动能定理、动量守恒定律、能量守恒定律即可正确解题,解题时要注意准确选择研究过程,注意正方向的选择.

 如图所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且 垂直纸面,MN、PQ为其边界,OO′为其对称轴.一导线折成边长为L的正方形闭合回路abcd,回路在纸面内以恒定速度v0向右运动,当运动到关于OO′对称的位置时( )
如图所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且 垂直纸面,MN、PQ为其边界,OO′为其对称轴.一导线折成边长为L的正方形闭合回路abcd,回路在纸面内以恒定速度v0向右运动,当运动到关于OO′对称的位置时( )| A. | 穿过回路的磁通量为零 | |
| B. | 回路中感应电动势大小为BLv0 | |
| C. | 回路中感应电流的方向为顺时针方向 | |
| D. | 回路中ab边与cd边所受安培力方向相同 |
 滑块沿倾角均为θ的轨道1和2下滑,滑块下用细绳悬吊一重物,滑块在下滑过程中某一时刻的速度均为v,轨道1上悬绳与竖直方向的夹角为θ,轨道2上悬绳与斜面的夹角为$\frac{π}{2}$-θ,如图所示,设滑块与轨道1和2的动摩擦因数分为μ1和μ2,则( )
滑块沿倾角均为θ的轨道1和2下滑,滑块下用细绳悬吊一重物,滑块在下滑过程中某一时刻的速度均为v,轨道1上悬绳与竖直方向的夹角为θ,轨道2上悬绳与斜面的夹角为$\frac{π}{2}$-θ,如图所示,设滑块与轨道1和2的动摩擦因数分为μ1和μ2,则( )| A. | μ1=0,0<μ2<tanθ | B. | μ1=0,μ2=tanθ | C. | 0<μ1<tanθ,μ2=0 | D. | μ1>tanθ,μ2=0 |
 如图,足够长的光滑导轨倾斜放置,导轨宽度为l,下端与电阻R连接,其它电阻不计,匀强磁场垂直于导轨平面向上.若金属棒ab以一定初速度v0沿导轨下滑,则棒( )
如图,足够长的光滑导轨倾斜放置,导轨宽度为l,下端与电阻R连接,其它电阻不计,匀强磁场垂直于导轨平面向上.若金属棒ab以一定初速度v0沿导轨下滑,则棒( )| A. | 电流方向从a到b | |
| B. | 刚开始下滑瞬间产生的电动势为Blv0 | |
| C. | 最终能匀速下滑 | |
| D. | 减少的重力势能全部等于电阻R产生的内能 |
| A. | 平均速度 | B. | 电场强度 | C. | 磁感应强度 | D. | 电流强度 |
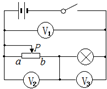 如图,电源电动势为3V,内阻不可忽略,滑动变阻器的滑片P从a滑向b的过程中,三只理想电压表的示数变化的绝对值分别为△U1、△U2、△U3,下列各值不可能出现的是( )
如图,电源电动势为3V,内阻不可忽略,滑动变阻器的滑片P从a滑向b的过程中,三只理想电压表的示数变化的绝对值分别为△U1、△U2、△U3,下列各值不可能出现的是( )| A. | △U1=3V、△U2=2V、△U3=1V | B. | △U1=1V、△U2=3V、△U3=2V | ||
| C. | △U1=0.5V、△U2=1V、△U3=1.5V | D. | △U1=0.2V、△U2=1V、△U3=0.8V |
 如图,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=30kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求:
如图,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=30kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求: 由粗细两段组成的管道固定在竖直平面内,粗、细管横截面积分别为2S、S.细管底部由光滑“工”字型轻活塞封闭.初始时细管内水银柱和被封闭气体位置尺寸如图所示,水银上表面恰位于粗细管连接处.外界大气压p0=76cmHg柱:
由粗细两段组成的管道固定在竖直平面内,粗、细管横截面积分别为2S、S.细管底部由光滑“工”字型轻活塞封闭.初始时细管内水银柱和被封闭气体位置尺寸如图所示,水银上表面恰位于粗细管连接处.外界大气压p0=76cmHg柱: