题目内容
【题目】在一倾角为![]() 的光滑绝缘斜面上方,有平行于斜面向上的匀强电场,虚线MN为电场的上边界,场强大小E=
的光滑绝缘斜面上方,有平行于斜面向上的匀强电场,虚线MN为电场的上边界,场强大小E=![]() V/m,MN上方有一长为L=0.5 m的轻质绝缘杆,杆的上下两端分别固定一个小球A、B(可看成质点),质量均为m=0.01 kg,A不带电,B带电荷量-q2=
V/m,MN上方有一长为L=0.5 m的轻质绝缘杆,杆的上下两端分别固定一个小球A、B(可看成质点),质量均为m=0.01 kg,A不带电,B带电荷量-q2=![]() C,B到MN的距离d=0.4 m.现将A、B两球由静止释放(g取10 m/s2),求:
C,B到MN的距离d=0.4 m.现将A、B两球由静止释放(g取10 m/s2),求:
(1)小球B在匀强电场中,而A还未进入电场时,两小球的加速度大小;
(2)从开始运动到A刚要进入匀强电场过程的时间。

【答案】(1)10m/s2 (2) 0.6 s
【解析】
(1)以A、B球以及杆整体做研究对象,由牛顿第二定律:
2mgsin30°+q2E =2ma
解得:a=10m/s2
(2)B未进入电场前,设系统的加速度为a1,时间为t1,由牛顿第二定律有
![]()
![]()
解得t1=0.4 s
B球进入电场瞬间的速度为
![]()
从B球进入电场至A球刚要进入电场,设这段时间为t2,由运动学公式
![]()
解得t2=0.2 s
从开始运动,至A球刚要进入电场的时间为
t=t1+t2=0.6 s.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出0、1、2、3、4、5、6共7个测量点。其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为![]() ,完成下面问题。
,完成下面问题。
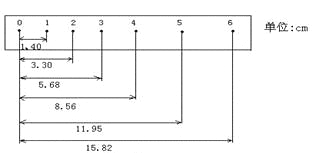
(1)根据打点计时器打出的纸带,我们可以直接得到的物理量是
A.时间间隔 | B.加速度 |
C.瞬时速度 | D.平均速度 |
(2)根据纸带上各个测量点间的距离,某同学已将1、2、3、5点对应的时刻的瞬时速度进行计算
并填入表中,请你将4点对应的时刻的瞬时速度填入表中;(要求保留3位有效数字)
瞬时速度 | v1 | v2 | v3 | v4 | v5 |
数值(m/s) | 0.165 | 0.214 | 0.263 | 0.363 |
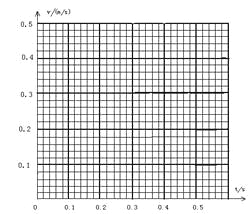
(3)在图所示的直角坐标系中画出小车的瞬时速度随时间变化的关系图线。
(4)由图像求出小车的加速度![]()