题目内容
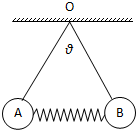如图所示，A、B两球完全相同，质量均为m，用两根等长的细线悬挂在O点，两球之间固连着一根劲度系数为k的轻弹簧，两球静止时，弹簧位于水平方向且与AB两球心连线共线，两根细线之间的夹角为θ，求：（1）细线中拉力的大小；
（2）弹簧长度的压缩量．
分析：对A球受力分析，然后根据平衡条件并运用合成法得到弹簧的弹力和细线的拉力，最后根据胡克定律得到弹簧的压缩量．
解答：解：对球A受力分析，受重力mg、拉力T、弹簧的弹力F，如图
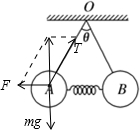
根据平衡条件，结合合成法，有：
T=
F=mgtan
根据胡克定律，有：
F=kx
k△x=mgtan
；
所以弹簧长度的压缩量：△x=
答：（1）细线中拉力的大小 T=
；
（2）所以弹簧长度的压缩量为
．
根据平衡条件，结合合成法，有：
T=
| mg | ||
cos
|
F=mgtan
| θ |
| 2 |
根据胡克定律，有：
F=kx
k△x=mgtan
| θ |
| 2 |
所以弹簧长度的压缩量：△x=
mgtan
| ||
| k |
答：（1）细线中拉力的大小 T=
| mg | ||
cos
|
（2）所以弹簧长度的压缩量为
mgtan
| ||
| k |
点评：本题关键是对小球受力分析，然后根据共点力平衡条件并运用合成法求解出弹力，最后根据胡克定律求解出弹簧的压缩量．
练习册系列答案
阅读快车系列答案
相关题目
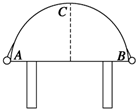如图所示，A、B两球质量分别为4m和5m，其间用轻绳连接，跨放在光滑的半圆柱体上（半圆柱体的半径为R）．两球从水平直径的两端由静止释放．已知重力加速度为g，圆周率用π表示．当球A到达最高点C时，求：
如图所示，A、B两球质量相同，悬线长度LA＞LB，将它们的悬线都拉至同一水平位置后，无初速释放，则两小球摆到最低点时：（取同一零势能参考面）（ ）
如图所示，A、B两球用细线悬挂于天花板上且静止不动，两球质量mA=2mB，两球间是一个轻质弹簧，如果突然剪断悬线，则在剪断悬线瞬间（ ）
如图所示，A、B两球用劲度系数为k1的轻弹簧相连，A被固定在竖直支架上，A点正上方的点O悬有一轻绳拉住B球，平衡时绳长为L，张力为T1．若将弹簧换成劲度系数为k2的轻弹簧，再次平衡时绳中的张力为T2，则T1、T2的关系是（ ）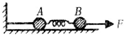
如图所示，A、B两球质量均为m，它们之间用轻弹簧连接，放在光滑的水平地面上，A球与墙之间有一不可伸长的细绳，B球受到水平向右的拉力F，A、B两球均处于静止状态．现突然撤去拉力F，此瞬间A、B的加速度aA、aB的大小是（ ）