题目内容
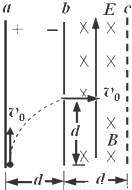
如图所示,两块足够大的平行金属板a、b竖直放置,板间有场强为E的匀强电场,两板距离为d,今有一带正电微粒从a板下边缘以初速度v竖直向上射入板间,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感应强度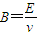 ,方向垂直纸面向里.求:
,方向垂直纸面向里.求:(1)微粒的带电量q;
(2)微粒穿出bc区域的位置到a板下边缘的竖直距离L(用d表示);
(3)微粒在ab、bc区域中运动的总时间t(用d、v表示).
【答案】分析:(1)将粒子的运动分解为水平方向和竖直方向,根据两个方向上的运动规律,抓住等时性求出微粒的带电量.
(2)根据第一问可知,粒子电场力和重力平衡,则粒子在bc区域内做匀速圆周运动.根据洛伦兹力提供向心力求出粒子做圆周运动的半径,结合几何关系求出微粒穿出bc区域的位置到a板下边缘的竖直距离L.
(3)根据粒子在ab区域内水平方向上做匀加速直线运动,根据平均速度公式求出运动的时间,通过粒子在磁场中做圆周运动的圆心角求出粒子在磁场中运动的时间,从而求出总时间.
解答:解:(1)微粒在电场中受水平向右的电场力和竖直向下的重力,其运动分解为水平和竖直方向的匀变速运动.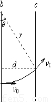
水平方向上的加速度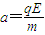 ,
,
又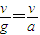
解得q=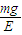 .
.
(2)微粒进入bc区域中由于电场力与重力平衡,微粒在洛伦兹力作用下做匀速圆周运动
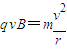
又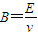 ,d=
,d=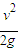
得圆周半径r=2d
微粒刚进入bc时洛伦兹力方向向上,逆时针偏转,轨迹如图所示,设圆心角为θ,有几何关系得,
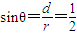 ,即θ=30°.
,即θ=30°.
微粒穿出bc区域的位置到a板下边缘的竖直距离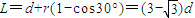 .
.
(3)微粒在电场中的运动时间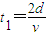
磁场中运动的时间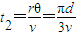
在ab、bc区域中运动的总时间t=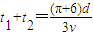 .
.
答:(1)微粒的带电量q=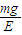 .
.
(2)微粒穿出bc区域的位置到a板下边缘的竖直距离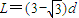 .
.
(3)微粒在ab、bc区域中运动的总时间t=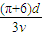 .
.
点评:本题关键是将粒子在电场中的运动正交分解为直线运动来研究,而粒子在复合场中运动时,重力和电场力平衡,洛仑兹力提供向心力,粒子做匀速圆周运动.
(2)根据第一问可知,粒子电场力和重力平衡,则粒子在bc区域内做匀速圆周运动.根据洛伦兹力提供向心力求出粒子做圆周运动的半径,结合几何关系求出微粒穿出bc区域的位置到a板下边缘的竖直距离L.
(3)根据粒子在ab区域内水平方向上做匀加速直线运动,根据平均速度公式求出运动的时间,通过粒子在磁场中做圆周运动的圆心角求出粒子在磁场中运动的时间,从而求出总时间.
解答:解:(1)微粒在电场中受水平向右的电场力和竖直向下的重力,其运动分解为水平和竖直方向的匀变速运动.

水平方向上的加速度
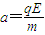 ,
,又
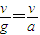
解得q=
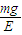 .
.(2)微粒进入bc区域中由于电场力与重力平衡,微粒在洛伦兹力作用下做匀速圆周运动
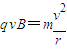
又
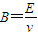 ,d=
,d=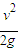
得圆周半径r=2d
微粒刚进入bc时洛伦兹力方向向上,逆时针偏转,轨迹如图所示,设圆心角为θ,有几何关系得,
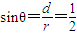 ,即θ=30°.
,即θ=30°.微粒穿出bc区域的位置到a板下边缘的竖直距离
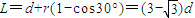 .
.(3)微粒在电场中的运动时间
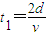
磁场中运动的时间
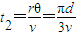
在ab、bc区域中运动的总时间t=
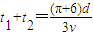 .
.答:(1)微粒的带电量q=
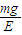 .
.(2)微粒穿出bc区域的位置到a板下边缘的竖直距离
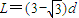 .
.(3)微粒在ab、bc区域中运动的总时间t=
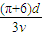 .
.点评:本题关键是将粒子在电场中的运动正交分解为直线运动来研究,而粒子在复合场中运动时,重力和电场力平衡,洛仑兹力提供向心力,粒子做匀速圆周运动.

练习册系列答案
相关题目
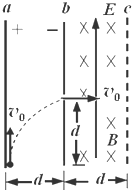 如图所示,两块足够大的平行金属板a、b竖直放置,板间有场强为E的匀强电场,两板距离为d,今有一带正电微粒从a板下边缘以初速度v0竖直向上射入板间,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感应强度
如图所示,两块足够大的平行金属板a、b竖直放置,板间有场强为E的匀强电场,两板距离为d,今有一带正电微粒从a板下边缘以初速度v0竖直向上射入板间,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感应强度

 ,方向垂直纸面向里。求:
,方向垂直纸面向里。求:
 ,方向垂直纸面向里。求:
,方向垂直纸面向里。求: