题目内容
 在中间位置有固定转动轴的长2l轻质杆两端固定两完全相同的质量为m、电荷量为+q的小球1和2,装置放在如图所示的关于竖直线对称的电场中,开始时杆在水平位置静止.现给小球1一个竖直向上的速度,让小球1、2绕转动轴各自转动到B、A位置,A、B间电势差是U,小球1、2构成的系统动能减小量是( )
在中间位置有固定转动轴的长2l轻质杆两端固定两完全相同的质量为m、电荷量为+q的小球1和2,装置放在如图所示的关于竖直线对称的电场中,开始时杆在水平位置静止.现给小球1一个竖直向上的速度,让小球1、2绕转动轴各自转动到B、A位置,A、B间电势差是U,小球1、2构成的系统动能减小量是( )A、一定大于
| ||
| B、一定等于2(Uq+mgl) | ||
| C、一定小于Uq | ||
| D、一定大于Uq+mgl |
分析:分析电场力和重力做功,根据动能定理求解系统动能减小量.电场力做功由公式W=qU和U=Ed定性分析.
解答:解:杆由水平位置转到竖直位置的过程中,重力对系统做功为0;
根据对称性知开始时两个小球处于同一等势面上,转动后,小球1所在位置的电势较低,电势能减少,小球2所在位置的电势较高,根据等势面线电场线的关系知道,A、2间电势差大于1、B间的电势差,小球2的电势升高量大于小球1电势降低量,所以小球2的电势能增加超过
qU,系统的重力势能未变,则动能减少,由能量守恒可知,系统动能减小量一定小于Uq.故C正确.
故选:C
根据对称性知开始时两个小球处于同一等势面上,转动后,小球1所在位置的电势较低,电势能减少,小球2所在位置的电势较高,根据等势面线电场线的关系知道,A、2间电势差大于1、B间的电势差,小球2的电势升高量大于小球1电势降低量,所以小球2的电势能增加超过
| 1 |
| 2 |
故选:C
点评:本题关键要能正确分析小球能量如何转化,运用W=qU和U=Ed定性分析两球电势能的变化关系,由能量守恒定律分析即可.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
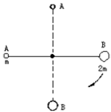 如图,质量分别为m和2m的两个小球A和B,中间用轻质杆相连,在杆的中点O处有一固定转动轴,把杆置于水平位置后释放,在B球顺时针摆动到最低位置的过程中( )
如图,质量分别为m和2m的两个小球A和B,中间用轻质杆相连,在杆的中点O处有一固定转动轴,把杆置于水平位置后释放,在B球顺时针摆动到最低位置的过程中( )| A、杆对球的力沿杆方向 | B、杆对A球做正功,杆对B球做负功 | C、A球、B球、杆和地球组成的系统机械能守恒 | D、重力对A球做功的瞬时功率一直变大 |
 在中间位置有固定转动轴的长为2l的轻质杆两端固定两个质量均为m、电荷量大小均为q的小球1和2,装置放在如图所示的关于竖直线对称的电场中,开始时杆在水平位置静止.现给小球1一个竖直向上的速度,让小球1、2绕转动轴各自转动到B、A位置,A、B间电势差是U,则在这一过程中小球1、2构成的系统( )
在中间位置有固定转动轴的长为2l的轻质杆两端固定两个质量均为m、电荷量大小均为q的小球1和2,装置放在如图所示的关于竖直线对称的电场中,开始时杆在水平位置静止.现给小球1一个竖直向上的速度,让小球1、2绕转动轴各自转动到B、A位置,A、B间电势差是U,则在这一过程中小球1、2构成的系统( )A、若两小球均带正电,动能变化量一定大于
| ||
| B、若两小球均带负电,动能变化量一定等于Uq+mgl | ||
| C、若球1带正电、球2带负电,动能变化量一定等于Uq | ||
| D、若两小球均带正电,动能变化量一定小于Uq |
如图,质量分别为m和2m的两个小球A和B,中间用轻质杆相连,在杆的中点O处有一固定转动轴,把杆置于水平位置后释放,在B球顺时针摆动到最低位置的过程中( )
| A.杆对球的力沿杆方向 |
| B.杆对A球做正功,杆对B球做负功 |
| C.A球、B球、杆和地球组成的系统机械能守恒 |
| D.重力对A球做功的瞬时功率一直变大 |