题目内容
如图所示,与水平面成θ=37°的光滑斜面与一光滑圆轨道相切于A点,斜面AB的长度 s=2.3m.让物体(可视为质点)从B点静止释放,恰能沿轨道运动到圆轨道的最高点C,空气阻力忽略不计(取sin37°=0.6,cos37°=0.8),(1)求圆轨道的半径R.
(2)设物体从C点落回斜面AB上的P点,试通过计算判断P位置比圆心O高还是低.

【答案】分析:(1)物体在最高点C时只受重力,则有mg=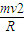 ,物体从B至C的过程中根据动能定理列式,联立方程即可求解;
,物体从B至C的过程中根据动能定理列式,联立方程即可求解;
(2)设物体一直平抛至与O等高处,根据平抛运动的特点求出水平位移,跟图中O到斜面的水平距离进行比较得出结论.
解答:解:(1)物体在最高点C时只受重力,根据 mg=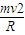
得物体在最高点C的速度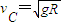
物体从B至C的过程中根据动能定理得: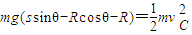
代入数据,解方程组,得R=0.6 m
(2)设物体一直平抛至与O等高处,则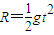 ,
,
水平位移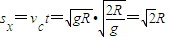
又由图可得O到斜面的水平距离为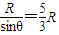 >sx
>sx
所以物体的落点位置P低于O.
答:(1)求圆轨道的半径R为0.6m.
(2)物体的落点位置P低于O.
点评:本题主要考查了动能定理及向心力公式的直接应用,要求同学们能根据需要选择适当的过程运用动能定理解题,难度适中.
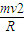 ,物体从B至C的过程中根据动能定理列式,联立方程即可求解;
,物体从B至C的过程中根据动能定理列式,联立方程即可求解;(2)设物体一直平抛至与O等高处,根据平抛运动的特点求出水平位移,跟图中O到斜面的水平距离进行比较得出结论.
解答:解:(1)物体在最高点C时只受重力,根据 mg=
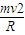
得物体在最高点C的速度
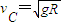
物体从B至C的过程中根据动能定理得:
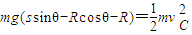
代入数据,解方程组,得R=0.6 m
(2)设物体一直平抛至与O等高处,则
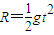 ,
,水平位移
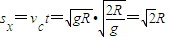
又由图可得O到斜面的水平距离为
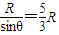 >sx
>sx 所以物体的落点位置P低于O.
答:(1)求圆轨道的半径R为0.6m.
(2)物体的落点位置P低于O.
点评:本题主要考查了动能定理及向心力公式的直接应用,要求同学们能根据需要选择适当的过程运用动能定理解题,难度适中.

练习册系列答案
相关题目
 如图所示,与水平面成θ角的皮带传送机,把质量为m的物体以速度v匀速向上传送,皮带作用于物体的摩擦力大小为
如图所示,与水平面成θ角的皮带传送机,把质量为m的物体以速度v匀速向上传送,皮带作用于物体的摩擦力大小为 如图所示,与水平面成37°角的传送带AB长16m,以10m/s的速度匀速运动,现将一质量为0.5kg的物体放于传送带A端由静止释放,已知物体与传送带之间的摩擦因数为0.5,求该物体运动到B端的时间.
如图所示,与水平面成37°角的传送带AB长16m,以10m/s的速度匀速运动,现将一质量为0.5kg的物体放于传送带A端由静止释放,已知物体与传送带之间的摩擦因数为0.5,求该物体运动到B端的时间. 如图所示,与水平面成37°的倾斜轨道AB,其延长线在C点与半圆轨道CD(轨道半径R=1m)相切,全部轨道为绝缘材料制成且放在竖直面内.整个空间存在水平向左的匀强电场,MN的右侧存在垂直纸面向里的匀强磁场.一个质量为0.4kg的带电小球沿斜面下滑,至B点时速度为VB=100/7 m/s,接着沿直线BC(此处无轨道)运动到达C处进入半圆轨道,进入时无动能损失,且刚好到达D点,从D点飞出时磁场消失,不计空气阻力,取g=10m/s2,cos37°=0.8,求:
如图所示,与水平面成37°的倾斜轨道AB,其延长线在C点与半圆轨道CD(轨道半径R=1m)相切,全部轨道为绝缘材料制成且放在竖直面内.整个空间存在水平向左的匀强电场,MN的右侧存在垂直纸面向里的匀强磁场.一个质量为0.4kg的带电小球沿斜面下滑,至B点时速度为VB=100/7 m/s,接着沿直线BC(此处无轨道)运动到达C处进入半圆轨道,进入时无动能损失,且刚好到达D点,从D点飞出时磁场消失,不计空气阻力,取g=10m/s2,cos37°=0.8,求: 如图所示,与水平面成30°角的光滑杆上套有一个小球和两根轻弹簧a、b,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定在杆上,小球处于静止状态,设拔去销钉M瞬间a弹力消失,小球加速度大小为20m/s2,那么不拔去销钉M而拔出销钉N的瞬间,小球加速度的值可能为(取 g=10m/s2)( )
如图所示,与水平面成30°角的光滑杆上套有一个小球和两根轻弹簧a、b,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定在杆上,小球处于静止状态,设拔去销钉M瞬间a弹力消失,小球加速度大小为20m/s2,那么不拔去销钉M而拔出销钉N的瞬间,小球加速度的值可能为(取 g=10m/s2)( ) 如图所示,与水平面成θ角的皮带传送机,把质量为m的货箱放到向上传送的皮带上,皮带的运转是匀速的,皮带与货箱间的动摩擦因数为μ,货箱从底端放上皮带时的速度为零,到达顶端前已经和皮带相对静止,货箱与皮带间相对运动阶段,货箱受到的摩擦力大小为
如图所示,与水平面成θ角的皮带传送机,把质量为m的货箱放到向上传送的皮带上,皮带的运转是匀速的,皮带与货箱间的动摩擦因数为μ,货箱从底端放上皮带时的速度为零,到达顶端前已经和皮带相对静止,货箱与皮带间相对运动阶段,货箱受到的摩擦力大小为