Question

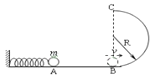
【题目】如图所示，AB是竖直平面内的四分之一光滑圆弧轨道，在下端B与水平直轨道相切，一小球自A点起由静止开始沿轨道下滑，已知圆轨道半径为h，小球的质量为m．

(1)求小球运动到B点时的速度；

(2)小球刚经过圆弧轨道的B点时，所受轨道支持力FB是多大？

(3)若小球与水平轨道之间的动摩擦因数为μ，小球与C点固定的竖直挡板只发生一次无机械能损失的碰撞后，最终停止在水平轨道上某处，BC长度为s，求物块停止的地方与B点距离的可能值．

Answer 1

【答案】(1), 方向为沿BC方向 (2)FB=3mg (3) 或

【解析】

（1）在下滑的过程中根据机械能守恒求得到达B点的速度；
（2）在B点根据牛顿第二定律求得作用力；
（3）整个过程根据动能定理求得在摩擦力作用下通过的路程，即可判断位置

（1）根据机械能守恒得 mgh＝mvB2
解得 vB＝,方向沿BC方向
（ 2）根据牛顿运动定律，在B点FBmg＝，

解得 F B=3mg
（ 3）设物块的质量为m，在水平轨道上滑行的总路程为s′由功能关系得
mgh=μmgs′
解得 s′=

第一种可能是：物块与弹性挡板碰撞后，在B前停止，物块停止的位置距B的距离为：d=2s-s′=2s-　　
第二种可能是：物块与弹性挡板碰撞后，可再一次滑上光滑圆弧轨道，滑下后在水平轨道上停止，则物块停止的位置距B的距离为：d=s′-2s=-2s