��Ŀ����
����Ŀ����ͼ��ʾ��ABΪ�̶�����ֱƽ���ڵ� ![]() �⻬Բ������������B����ˮƽ�������У���뾶ΪR������Ϊm��С����A�㾲ֹ�ͷţ��������ٶ�Ϊg����
�⻬Բ������������B����ˮƽ�������У���뾶ΪR������Ϊm��С����A�㾲ֹ�ͷţ��������ٶ�Ϊg����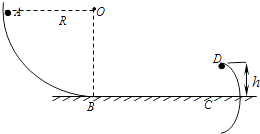
��1��С����͵�Bʱ��С���ٶ�v�Ĵ�С��
��2��С��յ�����͵�Bʱ�������С���֧����FN�Ĵ�С��
��3��С��ͨ���⻬��ˮƽ��BC���Ϲ̶���Բ�������ǡ�õ����Բ��ߵ�D��D������ĸ߶�Ϊh����֪h��R������С���ڰ�Բ������Ͽ˷�Ħ���������Ĺ�Wf�Ĵ�С��
���𰸡�
��1��
�⣺С����͵�����У��ɶ��ܶ����ã�mgR= ![]() mv2��0����ã�v=
mv2��0����ã�v= ![]()
��2��
�⣺��B�㣬��ţ�ٵڶ����ɵã�FN��mg=m ![]() ����ã�FN=3mg����С��յ�����͵�Bʱ�������С��֧����FN�Ĵ�СΪ3mg��
����ã�FN=3mg����С��յ�����͵�Bʱ�������С��֧����FN�Ĵ�СΪ3mg��
��3��
�⣺С��ǡ�õ���D�㣬��D�������ṩ����������ţ�ٵڶ����ɵã�mg=m ![]() ����A��D���������̣��ɶ��ܶ����ã�mgR��mgh��Wf=
����A��D���������̣��ɶ��ܶ����ã�mgR��mgh��Wf= ![]() mvD2��0��0����ã�Wf=mgR��
mvD2��0��0����ã�Wf=mgR�� ![]() mgh��
mgh��
����������1��С���A����B�Ĺ����У�֧������������ֻ���������������ݻ�е���غ㶨�ɻ��ܶ�����ʽ��⣻��2����Բ����͵�B��С������������֧�����ĺ����ṩ������������ţ�ٵڶ�������ʽ��⼴�ɣ���3����ţ�ٵڶ��������С��D���ٶȣ�Ȼ���ɶ��ܶ�������˷�Ħ���������Ĺ���
�����㾫����������Ҫ�������������Ͷ��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ��������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�