题目内容
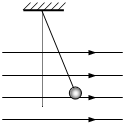
用L=30cm的细线将质量为m=4×10-3㎏的带电小球P悬挂在O点下，当空中有方向水平向右，大小为E=1×104N/C的匀强电场时，小球偏离竖直方向37°角后处于静止状态．（g=10m/s2，sin37°=0.6，cos37°=0.8）（1）分析小球的带电性质？
（2）求小球的带电量？
（3）剪断细线1s，小球发生的位移？
分析：根据共点力平衡得出小球所受电场力方向，确定出小球的电性，以及电量的大小．剪断细线后，小球做匀加速直线运动，根据牛顿第二定律求出加速度的大小，从而根据位移时间公式求出小球的位移．
解答：解：（1）小球受力与场强相同，故带正电．
（2）小球受力平衡，在水平方向：
qE=mgtan37°，得
q=
=3×10-6C．
（3）如受力图可知F=
=ma
a=12.5m/s2
线断后小球做匀加速直线运动s=
at2=6.25m．
答：（1）小球带正电．
（2）小球的带电量为3×10-6C．
（3）剪断细线1s，小球发生的位移为6.25m．
（2）小球受力平衡，在水平方向：
qE=mgtan37°，得
q=
| mgtan37° |
| E |
（3）如受力图可知F=
| mg |
| cos37° |
a=12.5m/s2
线断后小球做匀加速直线运动s=
| 1 |
| 2 |
答：（1）小球带正电．
（2）小球的带电量为3×10-6C．
（3）剪断细线1s，小球发生的位移为6.25m．
点评：解决本题的关键能够正确地受力分析，运用共点力平衡和牛顿第二定律进行求解，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
阅读快车系列答案
相关题目
用L=30cm的细线将质量为m=4×10-3㎏的带电小球P（可视为点电荷）悬挂在天花板下，当空中有方向为水平向右，大小为1×104N/C的匀强电场时（电场范围足够大），小球处于静止状态时细线与竖直方向成37°．（g取10m/s2，sin37°=0.6，cos37°=0.8）
（12分）用L=30cm的细线将质量为m=4×10-3㎏的带电小球P悬挂在Ｏ点下，当空中有方向水平向右，大小为E=1×104N/C的匀强电场时，小球偏离竖直方向37°角后处于静止状态。（g=10m/s2，
）
（12分）用L=30cm的细线将质量为m=4×10-3㎏的带电小球P悬挂在Ｏ点下，当空中有方向水平向右，大小为E=1×104N/C的匀强电场时，小球偏离竖直方向37°角后处于静止状态。（g=10m/s2，
）
取10m/s2，
，cos37o=0.8）