题目内容
 如图所示,边OA与OC之间分布有垂直纸面向里的匀强磁场,边OA上有一粒子源S,t=0瞬间粒子源从平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间运动后有相当数量的粒子会从边OC射出磁场.∠AOC=60°,已知从边OC射出的粒子在磁场中运动的最长时间等
如图所示,边OA与OC之间分布有垂直纸面向里的匀强磁场,边OA上有一粒子源S,t=0瞬间粒子源从平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间运动后有相当数量的粒子会从边OC射出磁场.∠AOC=60°,已知从边OC射出的粒子在磁场中运动的最长时间等| T |
| 2 |
分析:粒子在磁场中运动做匀速圆周运动,所有粒子的初速度大小相同,轨迹半径相同,弦越大,轨迹的圆心越大,运动时间越长.根据几何知识,画出轨迹,作出最长的弦,定出最长的运动时间.同理求解最短时间.即可得到时间范围.
解答: 解:设OS=d.
解:设OS=d.
粒子在磁场中运动做匀速圆周运动,所有粒子的速率相同,则轨迹的半径相同.入射点是S,出射点在OC直线上,出射点与S点的连线为轨迹的一条弦.当粒子轨迹的弦是直径时运动时间最长,根据几何知识,轨迹SD如图,则轨迹的直径为D=
d.当从边界OC射出的粒子在磁场中运动的时间最短时,轨迹的弦最短根据几何知识,作ES⊥OC,则ES为最短的弦,粒子从S到E的时间最短,由几何知识得,ES=
d=r,则圆心角θ=60°,故粒子在磁场中运动的最短时间为
.故在
-
时间内有粒子从边OC射出磁场.
故选BCD
 解:设OS=d.
解:设OS=d.粒子在磁场中运动做匀速圆周运动,所有粒子的速率相同,则轨迹的半径相同.入射点是S,出射点在OC直线上,出射点与S点的连线为轨迹的一条弦.当粒子轨迹的弦是直径时运动时间最长,根据几何知识,轨迹SD如图,则轨迹的直径为D=
| 3 |
| ||
| 2 |
| T |
| 6 |
| T |
| 6 |
| T |
| 2 |
故选BCD
点评:带电粒子在磁场中圆周运动的问题是高考的热点,也是难点,关键是运用几何知识画出轨迹.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目



 和
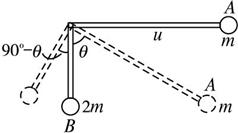
和 ,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则
,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则

