题目内容
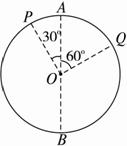
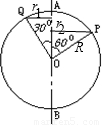
一圆环,其圆心为O,若以它的直径AB为轴做匀速转动,如图所示,(1)圆环上P、Q两点的线速度大小之比是______
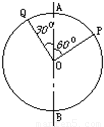
【答案】分析:(1)同一圆环以直径为轴做匀速转动时,环上的点的角速度相同,根据几何关系可以求得Q、P两点各自做圆周运动的半径,根据v=ωr即可求解线速度之比;
(2)根据a=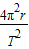 即可求得Q点的向心加速度大小.
即可求得Q点的向心加速度大小.
解答:解:P、Q两点以它的直径AB为轴做匀速转动,它们的角速度相同都为ω,
所以Q点转动的半径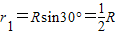 ,
,
P点转动的半径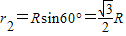
根据v=ωr得:
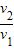 =
=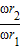 =
=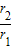 =
=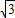
即圆环上P、Q两点的线速度大小之比是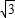 :1
:1
根据a=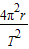 得:
得:
Q点的向心加速度大小为:a=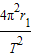 =4000π2m/s2
=4000π2m/s2
故答案为: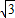 :1;4000π2m/s2
:1;4000π2m/s2
点评:该题主要考查了圆周运动基本公式的直接应用,注意同轴转动时角速度相同.
(2)根据a=
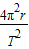 即可求得Q点的向心加速度大小.
即可求得Q点的向心加速度大小.解答:解:P、Q两点以它的直径AB为轴做匀速转动,它们的角速度相同都为ω,

所以Q点转动的半径
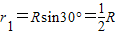 ,
,P点转动的半径
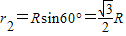
根据v=ωr得:
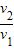 =
=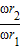 =
=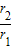 =
=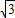
即圆环上P、Q两点的线速度大小之比是
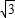 :1
:1根据a=
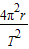 得:
得:Q点的向心加速度大小为:a=
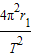 =4000π2m/s2
=4000π2m/s2故答案为:
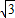 :1;4000π2m/s2
:1;4000π2m/s2点评:该题主要考查了圆周运动基本公式的直接应用,注意同轴转动时角速度相同.

练习册系列答案
相关题目
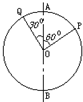 一圆环,其圆心为O,若以它的直径AB为轴做匀速转动,如图所示:
一圆环,其圆心为O,若以它的直径AB为轴做匀速转动,如图所示: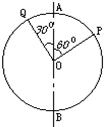 一圆环,其圆心为O,若以它的直径AB为轴做匀速转动,如图所示,
一圆环,其圆心为O,若以它的直径AB为轴做匀速转动,如图所示,