题目内容
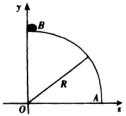
在光滑水平上，放置一个质量为M、截面是
圆(半径为R)的柱体A(如图)柱面光滑，顶端放一质量为m的小滑块B，初始时刻A、B都处于静止状态.在固定坐标系中(xOy)如图所示，设小滑块从圆柱顶端沿圆弧滑下，证明小滑块脱离圆弧以前在固定坐标系xOy中的轨迹为椭圆的一部分.
答案：
解析：
解析：
要证明小滑块m在离开柱体以前的轨迹为椭圆的一部分，必须求出滑块m的坐标方程.小滑块向右滑动的同时柱体向左滑动，系统水平向上动量守恒.
设下滑到某处时B的坐标为(x，y)，A的圆心C坐标为(x′，0).如图所示，A、B沿水平方向的速度分别是v′和v，则由水平方向的动量守恒可得 mv+Mv′=0 ① 此时B、C的水平坐标分别为x和x′，由于两物体的水平速率之比在任何时刻都相同，所以其水平方向的位移之比等于速率之比，从而 mx+Mx′=0 ② 在A脱离B之前，由几何关系可知
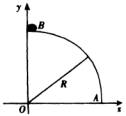
消去θ及x′，得B在脱离A之前的轨迹方程为
显然，B的轨迹是半长轴为R(在y方向)、半短轴为
|
③
(在x方向)的椭圆的一部分.
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
如图所示，在光滑水平地面上放置质量M=2kg的长木板，木板上表面与固定的竖直弧形轨道相切．一质量m=1kg的小滑块自A点沿弧面由静止滑下，A点距离长木板上表面高度h=0.6m．滑块在木板上滑行t=1s后，和木板以共同速度v=1m/s匀速运动，取g=10m/s2．求：
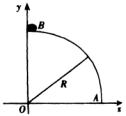
，在运动过程中只是B与墙壁碰撞，碰撞时间极短，且碰撞时无能量损失，取g=10m/s2，求：要使A最终不脱离B，木板B的最短长度是多少？
，在运动过程中只是B与墙壁碰撞，碰撞时间极短，且碰撞时无能量损失，取g=10m/s2，求：要使A最终不脱离B，木板B的最短长度是多少？