题目内容
9.如图所示,一轻质弹簧左端固定在A点,自然状态时其右端位于O点.水平向右侧有一竖直光滑圆形轨道在C点与水平面平滑连接,圆心为O′,半径R=0.4m.另一轻质弹簧一端固定在O′点的轴上,一端栓着一个小球,弹簧的原长为l0=0.5m,劲度系数k=100N/m.用质量m1=0.4kg的物体将弹簧缓慢压缩到B点(物体与弹簧不栓接),物块与水平面间的动摩擦因数μ=0.4,释放后物块恰运动到C点停止,BC间距离L=2m.换同种材料、质量m2=0.2kg的物块重复上述过程.(物块、小球均视为质点,g=10m/s2)求:
(1)物块m2到C点时的速度大小vC;
(2)若小球的质量也为m2,物块与小球碰撞后交换速度,论证小球是否能通过最高点D.若能通过,求出最高点轨道对小球的弹力N;若不能通过,求出小球离开轨道时的位置和O′连线与竖直方向的夹角θ(用三角函数值表示);
(3)在(2)问的基础上,若将拴着小球的弹簧换为劲度系数k′=10N/m的弹簧,再次求解.
分析 (1)从B到C有动能定理可求得到达C点速度;
(2)假设通过最高点,从C到D由动能定理求的D点速度,在D点由牛顿第二定律即可判断;
(3)假设通过最高点,从C到D由动能定理求的D点速度,在D点由牛顿第二定律即可判断,在利用动能定理即可求的夹角.
解答 解:(1)m1从B到C的过程:EP=μm1gL
m2从B到C的过程:EP=μm2gL+$\frac{1}{2}$m2vC2,解得:vC=4m/s
(2)碰后交换速度,小球以vC=4m/s向上运动,假设能到高点,
从C到D的过程:$\frac{1}{2}$m2vD2-$\frac{1}{2}$m2vC2=-m2g•2R,解得:vD=0m/s,
对D点:N+m2g-k(l0-R)=0,解得:N=8N,求解结果合理,
说明假设是正确的,小球可以通过最高点;
(3)假设能到高点,最高点弹力:N'+m2g-k'(l0-R)=0
解得:N=-1N,求解结果的不合理,说明假设是错误的,小球不可以通过最高点;
小球离开轨道时的位置E和O'连线与竖直方向的夹角θ,此时小球速度vE
由动能定理:$\frac{1}{2}$m2vE2-$\frac{1}{2}$m2vC2=m2g(R+Rcosθ)
对E点:m2gcosθ-k′(l0-R)=m2$\frac{{v}_{E}^{2}}{R}$,解得:cosθ=$\frac{5}{6}$,则θ=arccoa$\frac{5}{6}$;
答:(1)物块m2到C点时的速度大小vC为4m/s;
(2)若小球的质量也为m2,若物块与小球碰撞后交换速度,小球能通过最高点D.轨道最高点对小球的弹力N为8N;
(3)若将拴着小球的弹簧换为劲度系数k'=10N/m,小球不能通过最高点D.夹角为arccoa$\frac{5}{6}$.
点评 本题是动能定理与向心力公式的综合应用来处理圆周运动问题.利用功能关系解题的优点在于不用分析复杂的运动过程,只关心初末状态即可,平时要加强训练深刻体会这一点.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案| A. | 黑体辐射电磁波的强度按波长的分布不只与黑体的温度有关,还与材料有关 | |
| B. | 对于同种金属产生光电效应时,逸出光电子的最大初动能 Ek与照射光的频率成线性关系 | |
| C. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子的能量也减小了 | |
| D. | 将核子束缚在原子核内的核力,是不同于万有引力和电磁力的另一种相互作用 |
| A. | 牛顿利用斜面研究自由落体运动时,使用了“外推”的方法,即当斜面的倾角为90°时,物体在斜面上的运动就变成了自由落体运动 | |
| B. | 运动的合成与分解是研究曲线运动的一般方法,该方法不适用于研究匀速圆周运动 | |
| C. | 物理模型在物理学的研究中起了重要作用,其中“质点”、“点电荷”和“轻弹簧”都是理想化模型 | |
| D. | 库仑利用扭秤装置研究电荷间相互作用力的大小跟电荷量和距离的关系时,采用了理想实验法 |
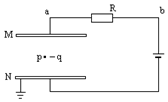 如图所示,在水平放置两平行金属板M、N之间的P点,固定有一个带电量为-q的点电荷,两金属板通过电阻R接到直流电源上,其中N板接地.( )
如图所示,在水平放置两平行金属板M、N之间的P点,固定有一个带电量为-q的点电荷,两金属板通过电阻R接到直流电源上,其中N板接地.( )| A. | 当保持其它条件不变,而将M板向上移动的过程中,两极板间的电场变强 | |
| B. | 当保持其它条件不变,而将M板向上移动的过程中,通过R的电流方向是向左的 | |
| C. | 当保持其它条件不变,而将M板向上移动到某处稳定后与移动前相比,p处点电荷的电势能变大 | |
| D. | 将电容器与电源断开,若M板向上移动到某处稳定后与移动前相比,p处点电荷的电势能变小 |
| A. | 12.5m | B. | 2m | C. | 10m | D. | 0m |

 如图所示,O为竖直放置的半径R=2m的光滑管状轨道圆心,A、B两点关于O的竖直线对称,从A点将质量为m=0.2kg的小球以某一速度斜向上抛出,无碰撞地由B点进入管道,小球经圆轨道最低点C无能量损失地进入长L=4m水平粗糙轨道CD,小球与CD间动摩擦因数μ=0.2,光滑半圆轨道DE竖直放置,E为最高点,G是与圆心O1等高的点,小球经D点无能量损失进入半圆轨道并能到达EG间某处,已知圆管的直径远小于轨道半径R且略大于小球直径,OB与竖直方向间夹角α=37°,(取sin37°=0.6,g取10m/s2)求:
如图所示,O为竖直放置的半径R=2m的光滑管状轨道圆心,A、B两点关于O的竖直线对称,从A点将质量为m=0.2kg的小球以某一速度斜向上抛出,无碰撞地由B点进入管道,小球经圆轨道最低点C无能量损失地进入长L=4m水平粗糙轨道CD,小球与CD间动摩擦因数μ=0.2,光滑半圆轨道DE竖直放置,E为最高点,G是与圆心O1等高的点,小球经D点无能量损失进入半圆轨道并能到达EG间某处,已知圆管的直径远小于轨道半径R且略大于小球直径,OB与竖直方向间夹角α=37°,(取sin37°=0.6,g取10m/s2)求: