题目内容
如图所示,水平台面AB距地面的高度h=0.80m.有一滑块从A点以v0=6.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.5.滑块运动到平台边缘的B点后水平飞出.已知AB=2.7m.不计空气阻力,g取10m/s2,求:
(1)滑块从B点飞出时的速度大小;
(2)滑块落地点到平台边缘的水平距离;
(3)滑块落地前瞬间的速度与水平方向的夹角(结果可直接用三角函数表示).
(1)滑块从B点飞出时的速度大小;
(2)滑块落地点到平台边缘的水平距离;
(3)滑块落地前瞬间的速度与水平方向的夹角(结果可直接用三角函数表示).

(1)设滑块到达B点的速度为vB,由动能定理得:
-μmgs=
nvB2-
mv02
故vB=
=
m/s=3m/s
(2)由平抛运动规律,竖直方向做自由落体运动,则
h=
g t2
所以t=
=0.4s
水平方向做匀速直线运动,x=vBt=3×0.4m=1.2m
即滑块落地点到平台边缘的水平距离为1.2m;
(3)落地前瞬间竖直速度为:
vy=gt=10×0.4m/s=4m/s
水平方向的速度为vB=3m/s,设速度与水平方向的夹角为α,
则 tanα=
=
.
答:(1)滑块从B点飞出时的速度大小为3m/s;(2)滑块落地点到平台边缘的水平距离为1.2m;(3)滑块落地前瞬间的速度与水平方向的夹角为tanα=
.
-μmgs=
| 1 |
| 2 |
| 1 |
| 2 |
故vB=
| v02-2μgs |
| 62- 2×0.5×10×2.7 |
(2)由平抛运动规律,竖直方向做自由落体运动,则
h=
| 1 |
| 2 |
所以t=
|
水平方向做匀速直线运动,x=vBt=3×0.4m=1.2m
即滑块落地点到平台边缘的水平距离为1.2m;
(3)落地前瞬间竖直速度为:
vy=gt=10×0.4m/s=4m/s
水平方向的速度为vB=3m/s,设速度与水平方向的夹角为α,
则 tanα=
| vy |
| vB |
| 4 |
| 3 |
答:(1)滑块从B点飞出时的速度大小为3m/s;(2)滑块落地点到平台边缘的水平距离为1.2m;(3)滑块落地前瞬间的速度与水平方向的夹角为tanα=
| 4 |
| 3 |

练习册系列答案
相关题目
 如图所示,水平台面AB距地面的高度h=0.80m.有一滑块从A点以v0=6.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.25.滑块运动到平台边缘的B点后水平飞出.已知AB=2.2m.不计空气阻力,g取10m/s2,结果保留2位有效数字.求:
如图所示,水平台面AB距地面的高度h=0.80m.有一滑块从A点以v0=6.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.25.滑块运动到平台边缘的B点后水平飞出.已知AB=2.2m.不计空气阻力,g取10m/s2,结果保留2位有效数字.求: (2012?潍坊模拟)如图所示,水平台面AB距地面CD高h=0.8m.有一滑块从A点以6.0m/s的初速度在平台上沿AB方向运动,并从平台边缘的B点水平飞出,最后落在地面上的D点.已知AB=2.20m,落地点到平台的水平距离为2.00m.(不计空气阻力,g取10m/s2)求滑块从A到D所用的时间和滑块与平台间的动摩擦因数.
(2012?潍坊模拟)如图所示,水平台面AB距地面CD高h=0.8m.有一滑块从A点以6.0m/s的初速度在平台上沿AB方向运动,并从平台边缘的B点水平飞出,最后落在地面上的D点.已知AB=2.20m,落地点到平台的水平距离为2.00m.(不计空气阻力,g取10m/s2)求滑块从A到D所用的时间和滑块与平台间的动摩擦因数. (2013?红桥区一模)如图所示,水平台面AB距地面的高度h=0.80m.质量为0.2kg的滑块以v0=6.0m/s的初速度从A点开始滑动,滑块与平台间的动摩擦因数μ=0.25.滑块滑到平台边缘的B点后水平飞出.已知AB间距离s1=2.2m.滑块可视为质点,不计空气阻力.(g取10m/s2)求:
(2013?红桥区一模)如图所示,水平台面AB距地面的高度h=0.80m.质量为0.2kg的滑块以v0=6.0m/s的初速度从A点开始滑动,滑块与平台间的动摩擦因数μ=0.25.滑块滑到平台边缘的B点后水平飞出.已知AB间距离s1=2.2m.滑块可视为质点,不计空气阻力.(g取10m/s2)求: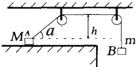 如图所示,水平台面光滑,穿过两光滑轻质定滑轮的轻绳两端分别连接着物体A和B,A、B的质量分别为M和m,滑轮到台面高为h,用手按住A此时A端绳与台面的夹角 a=30°,然后放手,使它们运动,已知A始终没有离开台面,则A的最大速度为( )
如图所示,水平台面光滑,穿过两光滑轻质定滑轮的轻绳两端分别连接着物体A和B,A、B的质量分别为M和m,滑轮到台面高为h,用手按住A此时A端绳与台面的夹角 a=30°,然后放手,使它们运动,已知A始终没有离开台面,则A的最大速度为( )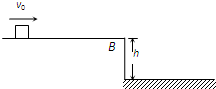 如图所示,水平台面AB距地面的高度h=0.8m.有一滑块从A点以初速度v0=6m/s的在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.25.滑块运动到平台边缘的B点后以速度vB水平飞出.已知AB=2.2m.不计空气阻力,g取10m/s2.求:
如图所示,水平台面AB距地面的高度h=0.8m.有一滑块从A点以初速度v0=6m/s的在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.25.滑块运动到平台边缘的B点后以速度vB水平飞出.已知AB=2.2m.不计空气阻力,g取10m/s2.求: