题目内容
8. 如图所示,三角形斜劈A放在斜面体B上,在沿斜面向下的力F作用下,A和B均处于静止状态.现逐渐增大力F,A和B仍保持静止,则( )
如图所示,三角形斜劈A放在斜面体B上,在沿斜面向下的力F作用下,A和B均处于静止状态.现逐渐增大力F,A和B仍保持静止,则( )| A. | A对B的压力增大 | B. | A受到的合力增大 | ||
| C. | 地面对B的支持力增大 | D. | A对B的作用力不变 |
分析 首先对A受力分析,结合平衡条件分析各个力的变化情况;再对A、B整体分析,同样可以根据平衡条件列式分析各个力的变化情况.
解答 解:ABD、对A受力分析,受重力、推力、支持力、静摩擦力,由于物体保持静止,故合力一直为零,保持不变,故B错误;
根据平衡条件,B对A的支持力等于其重力的垂直斜面的分力,为N=mgcosθ,保持不变,再根据牛顿第三定律,A对B的压力也保持不变,故A错误;
在平行斜面方向,根据平衡条件,有:f=F+mgcosθ,故静摩擦力f增加,静摩擦力和支持力N垂直,两个力的合力为$\sqrt{{f}^{2}+{N}^{2}}$,也增加,再根据牛顿第三定律,A对B的作用力增加,故D错误;
C、再对A与B整体分析,受推力、重力、支持力和地面的静摩擦力,地面支持力N′=(M+m)g+Fsinθ,由于F增加,故N′增加,故C正确;
故选:C
点评 本题关键是采用整体法和隔离法灵活选择研究对象,受力分析后根据破坏规矩并结合正交分解法列式分析,不难.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
18.关静电力与洛伦兹力,以下说法正确的是( )
| A. | 静电场中的电荷一定会受到静电力的作用,磁场中的运动电荷一定会受到洛伦兹力作用 | |
| B. | 静电力一定会对电场中的运动电荷做功,而洛伦兹力对磁场中的运动电荷则一定不做功 | |
| C. | 静电力方向与电场线方向平行,洛伦兹力方向也与磁感线方向平行 | |
| D. | 静电力和洛伦兹力的大小均与电荷量大小成正比 |
19. 如图为某小型水电站的电能输送示意图.已知发电机的输出电压为240V,输电线的总电阻R=16Ω,降压变压器T2的原、副线圈匝数之比为4:1,电阻R0=11Ω.若T1、T2均为理想变压器,T2的副线圈两端电压表达式为u=220$\sqrt{2}$sin 100πt V,下列说法正确的是( )
如图为某小型水电站的电能输送示意图.已知发电机的输出电压为240V,输电线的总电阻R=16Ω,降压变压器T2的原、副线圈匝数之比为4:1,电阻R0=11Ω.若T1、T2均为理想变压器,T2的副线圈两端电压表达式为u=220$\sqrt{2}$sin 100πt V,下列说法正确的是( )
 如图为某小型水电站的电能输送示意图.已知发电机的输出电压为240V,输电线的总电阻R=16Ω,降压变压器T2的原、副线圈匝数之比为4:1,电阻R0=11Ω.若T1、T2均为理想变压器,T2的副线圈两端电压表达式为u=220$\sqrt{2}$sin 100πt V,下列说法正确的是( )
如图为某小型水电站的电能输送示意图.已知发电机的输出电压为240V,输电线的总电阻R=16Ω,降压变压器T2的原、副线圈匝数之比为4:1,电阻R0=11Ω.若T1、T2均为理想变压器,T2的副线圈两端电压表达式为u=220$\sqrt{2}$sin 100πt V,下列说法正确的是( )| A. | 发电机中的电流变化频率为100 Hz | |
| B. | 升压变压器T1的原、副线圈匝数之比为1:4 | |
| C. | 升压变压器T1的输入功率为4800 W | |
| D. | 若R0的电阻减小,发电机的输出功率也减小 |
16.发光晶体二极管是用电器上做指示灯用的一种电子元件.它的电路符号如图甲所示,正常使用时,带“+”号的一端接高电势,“-”的一端接低电势.某同学用实验方法测得它的两端的电压U和通过它的电流I的关系数据如表所示.
(1)在图乙中的虚线框内画出该同学的实验电路图.(除电源、开关、滑动变阻器外,实验用电压表V:内阻RV约为10kΩ;电流表mA:内阻RA约为100Ω)
(2)在图丙中的小方格纸上用描点法画出二极管的伏安特性曲线.
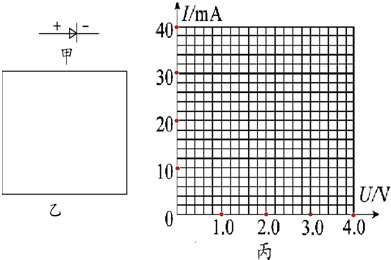
(3)若发光二极管的最佳工作电压为2.5V,而电源是由内阻不计、电动势为3V的供电系统提供的.请根据所画出的伏安特性曲线上的信息,分析应该串联一个阻值25Ω电阻再与电源接成闭合电路,才能使二极管工作在最佳状态.(结果保留二位有效数字)
| U/V | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 | 2.6 | 2.8 | 3.0 |
| I/mA | 0 | 0.9 | 2.3 | 4.3 | 6.8 | 12.0 | 19.0 | 24.0 | 30.0 | 37.0 |
(2)在图丙中的小方格纸上用描点法画出二极管的伏安特性曲线.

(3)若发光二极管的最佳工作电压为2.5V,而电源是由内阻不计、电动势为3V的供电系统提供的.请根据所画出的伏安特性曲线上的信息,分析应该串联一个阻值25Ω电阻再与电源接成闭合电路,才能使二极管工作在最佳状态.(结果保留二位有效数字)
17.如图为a、b两物体同时开始运动的图象,下列说法正确的是( )


| A. | 若图象为位置-时间图象,则两物体在M时刻相遇 | |
| B. | 若图象为速度-时间图象,则两物体在M时刻相距最远 | |
| C. | 若图象为加速度-时间图象,则两物体在M时刻速度相同 | |
| D. | 若图象为作用在两物体上的合力-位移图象,则两物体在M位移内动能增量相同 |
2. 如图所示,由一段外皮绝缘的导线扭成两个半径为R和r圆形平面形成的闭合回路,R>r,导线单位长度的电阻为λ,导线截面半径远小于R和r.圆形区域内存在垂直平面向里、磁感应强度大小随时间按B=kt(k>0,为常数)的规律变化的磁场,下列说法正确的是( )
如图所示,由一段外皮绝缘的导线扭成两个半径为R和r圆形平面形成的闭合回路,R>r,导线单位长度的电阻为λ,导线截面半径远小于R和r.圆形区域内存在垂直平面向里、磁感应强度大小随时间按B=kt(k>0,为常数)的规律变化的磁场,下列说法正确的是( )
 如图所示,由一段外皮绝缘的导线扭成两个半径为R和r圆形平面形成的闭合回路,R>r,导线单位长度的电阻为λ,导线截面半径远小于R和r.圆形区域内存在垂直平面向里、磁感应强度大小随时间按B=kt(k>0,为常数)的规律变化的磁场,下列说法正确的是( )
如图所示,由一段外皮绝缘的导线扭成两个半径为R和r圆形平面形成的闭合回路,R>r,导线单位长度的电阻为λ,导线截面半径远小于R和r.圆形区域内存在垂直平面向里、磁感应强度大小随时间按B=kt(k>0,为常数)的规律变化的磁场,下列说法正确的是( )| A. | 小圆环中电流的方向为逆时针 | B. | 大圆环中电流的方向为逆时针 | ||
| C. | 回路中感应电流大小为$\frac{k({R}^{2}+{r}^{2})}{λ(R+r)}$ | D. | 回路中感应电流大小为$\frac{k(R-r)}{2λ}$ |