题目内容
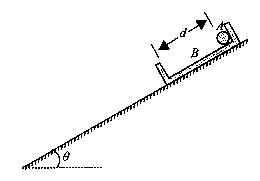
如图所示,在倾角![]() =30°的斜面上放置一段凹槽B,B与斜面间的动摩擦因数
=30°的斜面上放置一段凹槽B,B与斜面间的动摩擦因数![]() ,槽内靠近右侧壁处有一小球A,它到凹槽内左侧壁的距离
,槽内靠近右侧壁处有一小球A,它到凹槽内左侧壁的距离![]() .A、B的质量都为m=2.0kg.B与斜面间的最大静摩擦力可认为等于滑动摩擦力,不计A、B之间的摩擦,斜面足够长。现同刚由静止释放A、B,经过一段时间,A与B的侧壁发生碰撞, 碰撞过程不损失机械能,碰撞时间极短。取重力加速度g=10m/s。2求:
.A、B的质量都为m=2.0kg.B与斜面间的最大静摩擦力可认为等于滑动摩擦力,不计A、B之间的摩擦,斜面足够长。现同刚由静止释放A、B,经过一段时间,A与B的侧壁发生碰撞, 碰撞过程不损失机械能,碰撞时间极短。取重力加速度g=10m/s。2求:
(1)A与B的左侧壁第一次发生碰撞后瞬间A、B的速度。
 (2)在A与B的左侧壁发生第一次碰撞后到第二次碰撞前的这段时间内,A与B的左侧壁的距离最大可达到多少?
(2)在A与B的左侧壁发生第一次碰撞后到第二次碰撞前的这段时间内,A与B的左侧壁的距离最大可达到多少?
解:(1)A在凹槽内,B受到的滑动摩擦力
![]() ① …………2分
① …………2分
B所受重力沿斜面的分力
![]()
因为![]() ,所以B受力平衡,释放后B保持静止② …………1分
,所以B受力平衡,释放后B保持静止② …………1分
释放A后,A做匀加速运动,由牛顿和运动学规律得
![]() ③ …………1分
③ …………1分
![]() ④ …………分
④ …………分
解得A的加速度和碰撞前的速度分别为
![]() ⑤ …………1分
⑤ …………1分
A、B发生碰撞,动量守恒
![]() ⑥ …………2分
⑥ …………2分
碰撞过程不损失机械能,得
![]() ⑦ …………2分
⑦ …………2分
解得第一次发生碰撞后瞬间A、B的速度分别为
![]() (方向沿斜面向下)⑧ …………2分
(方向沿斜面向下)⑧ …………2分
(2)A、B第一次碰撞后,B做匀速运动![]() ⑨ …………1分
⑨ …………1分
A做匀加速运动,加速度仍为![]()
![]() ⑩ …………1分
⑩ …………1分
![]() (11) …………1分
(11) …………1分
经过时间t1,A的速度与B相等,A与B的左侧壁距离达到最大,即
![]() (12) …………1分
(12) …………1分
![]() (13) …………1分
(13) …………1分
代入数据解得A与B左侧壁的距离![]() (14) …………2分
(14) …………2分
因为s=d,A恰好运动到B的右侧壁,而且速度相等,所以A与B的右侧壁恰好接触但没有发生碰撞 (15) …………1分
因此A与B的左侧壁的距离最大可达到0.10m。

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案 如图所示,在倾角为θ的光滑固定斜面上,劲度系数分别为k1、k2的两个轻弹簧平行于斜面悬挂着,k1在上 k2在下,两弹簧之间有一质量为m1的重物,现用力F(未知)沿斜面向上缓慢推动m2,当两弹簧的总长等于两弹簧的原长之和时,
如图所示,在倾角为θ的光滑固定斜面上,劲度系数分别为k1、k2的两个轻弹簧平行于斜面悬挂着,k1在上 k2在下,两弹簧之间有一质量为m1的重物,现用力F(未知)沿斜面向上缓慢推动m2,当两弹簧的总长等于两弹簧的原长之和时, (2009?深圳一模)如图所示,在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG,图中OH∥CD∥FG,∠DEF=60°,CD=DE=EF=FG=OE=L;一根质量为m、长度为2L的导体棒AB在电机牵引下,以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端,O是AB棒的中点,AB⊥OH.金属导轨的CD、FG段电阻不计,DEF段与AB棒材料与横截面积均相同,单位长度的电阻均为r,整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中.求:
(2009?深圳一模)如图所示,在倾角为30°的光滑斜面上固定一光滑金属导轨CDEFG,图中OH∥CD∥FG,∠DEF=60°,CD=DE=EF=FG=OE=L;一根质量为m、长度为2L的导体棒AB在电机牵引下,以恒定速度v0沿OH方向从斜面底端滑上导轨并到达斜面顶端,O是AB棒的中点,AB⊥OH.金属导轨的CD、FG段电阻不计,DEF段与AB棒材料与横截面积均相同,单位长度的电阻均为r,整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中.求:

 如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为Q的正点电荷.O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=
如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为Q的正点电荷.O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=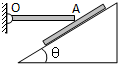 如图所示,在倾角θ 为37°的固定光滑斜面上放着一块质量不计的薄板,水平放置的棒OA,A端搁在薄板上,O端装有水平转轴,将薄板沿斜面向上和向下匀速拉动时所需拉力大小之比为3:4,则棒对板的压力大小之比为
如图所示,在倾角θ 为37°的固定光滑斜面上放着一块质量不计的薄板,水平放置的棒OA,A端搁在薄板上,O端装有水平转轴,将薄板沿斜面向上和向下匀速拉动时所需拉力大小之比为3:4,则棒对板的压力大小之比为