题目内容

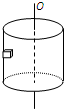
如图所示，半径为r的圆筒，绕竖直中心轴OO′旋转，小物块a靠在圆筒的内壁上，它与圆筒内壁间的动摩擦因数为μ，现要使a不下落，则圆筒转动的角速度ω至少为（　　）
A．
μgr
B．
μg
C．
g
r
D．
g
μr

要使A不下落，则小物块在竖直方向上受力平衡，有：f=mg
当摩擦力正好等于最大摩擦力时，圆筒转动的角速度ω取最小值，筒壁对物体的支持力提供向心力，
根据向心力公式得：N=mω2r
而f=μN
联立以上三式解得：ω=
g
μr
，故D正确．
故选：D．
练习册系列答案
相关题目
如图所示，一人用一根长1m，只能承受46N拉力的绳子，拴着一质量为1kg的小球，在竖直平面内作圆周运动，已知圆心O离地面h=6m．求：
（1）为使小球能在竖直平面内作完整的圆周运动，小球过最高点时的最小速度为多大？
（2）若在增加转动的速度使小球运动到最低点时绳子恰好断开，则绳子断时小球运动的线速度多大？
（3）绳断后，小球落地点与抛出点间的水平距离．（取g=10m/s2）
关于向心力的说法，正确的是（　　）
A．物体做匀速圆周运动时受到平衡力，向心力为零
B．向心力是指向圆心方向的合力，是根据力的作用效果来命名的
C．向心力既改变物体速度的方向，也改变物体速度的大小
D．向心力可以是重力、弹力、摩擦力等各种力的合力，也可以是其中某一个力或某一个力的分力
一辆质量2t的小轿车，驶过半径R=40m的一段圆弧形桥面，重力加速度g=10m/s2．求：
（1）若桥面为凹形，汽车以20m/s的速度通过桥面最低点时，对桥面压力是多大？
（2）若桥面为凸形，汽车以10m/s的速度通过桥面最高点时，对桥面压力是多大？
（3）汽车以多大速度通过凸形桥面顶点时，对桥面刚好没有压力？
如图所示，在甲、乙两个相同水平圆盘上，分别沿半径方向放置用长度相同细线相连质量均为m的小物体A（位于转轴处）、B和C、D，它们与圆盘之间的动摩擦因数相等．当甲、乙的角速度缓缓增大到A和B、C和D恰好将要相对圆盘滑动时，则下列说法中正确的是：（　　）
A．若突然剪断细线，A仍静止，B向外滑动
B．若突然剪断细线，C仍静止，D向外滑动动
C．若突然剪断细线，C、D均向外滑动
D．当角速度继续增加时，C、D将向外滑动
质量为1500kg的汽车以5m/s的速度驶过拱桥顶部．已知拱桥顶部的半径为50m．此时汽车的向心加速度大小为______，汽车对地面的压力大小为______．（g取10m/s2）
如图所示，用长为L的轻绳把一个铁球悬挂在高2L的O点处，小铁球以O为圆心在竖直平面内做圆周运动且恰能到达最高点B处，则有（　　）
A．小铁球在运动过程中轻绳的拉力最大为5mg
B．小铁球在运动过程中轻绳的拉力最小为mg
C．若运动中轻绳断开，则小铁球落到地面时的速度大小为
7gL
D．若小铁球运动到最低点轻绳断开，则小铁球落到地面时的水平位移为2L
飞行中的鸟要改变飞行方向时，鸟的身体要倾斜（如图所示）．与车辆不同的是，鸟转弯所需的向心力由重力和空气对它们的作用力的合力来提供．质量为m的飞鸟，以速率v在水平面内做半径为R的匀速圆周运动，空气对飞鸟作用力的大小等于（　　）
A．m
g2+
v4
R2
B．
mv2
R
C．m
v2
R2
-g2
D．mg
质量为5000kg的汽车以15m/s的速度驶过半径为30m的凸形桥，这时汽车对桥顶的压力是______N，当汽车速度为______m/s时，汽车对桥顶不再产生压力作用．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网