Question

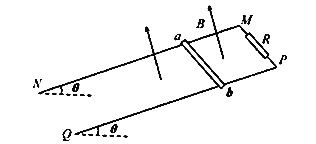
【题目】一长木板置于粗糙水平地面上，木板右端放置一小物块，如图所示。木板与地面间的动摩擦因数μ1=0.1，物块与木板间的动摩擦因数μ2=0.4。t=0时刻开始，小物块与木板一起以共同速度向墙壁运动，当t=1s时，木板以速度v1=4m/s与墙壁碰撞(碰撞时间极短)。碰撞前后木板速度大小不变，方向相反。运动过程中小物块第一次减速为零时恰好从木板上掉下。已知木板的质量是小物块质量的15倍，重力加速度大小g取10m/s2。求：

(1)t=0时刻木板的速度；

(2)木板的长度。

Answer 1

【答案】（1）（2）

【解析】

（1）对木板和物块：

令初始时刻木板速度为由运动学公式：

代入数据求得：

（2）碰撞后，对物块：

对物块，当速度为0时，经历时间t，发生位移x1，则有，

对木板，由牛顿第二定律：

对木板，经历时间t，发生位移x2

木板长度代入数据，