题目内容
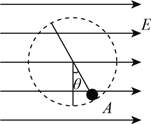
【题目】如图所示，在水平向右的匀强电场中，一个质量为
、电量为
的小球，用长为
的绝缘细线悬挂于
点，当小球静止在
点，此时细线与竖直方向夹角
．现给小球一个垂直于悬线的初速度，使小球恰好能在竖直平面内做圆周运动．试求：
（1）小球动能的最小值．
（2）小球在
点的初速度．
（3）小球机械能的最小值（设圆周运动的最低点为重力势能的零点）．
【答案】（1）
（2）
（3）
【解析】试题分析：对小球受力分析，求出等效重力，根据牛顿第二定律求出最小速度，进而求出小球动能的最小值；小球在原来静止点的速度最大，由动能定理可得小球在
点的初速度；设圆周运动的最低点为重力势能的零点，根据动能定理求出A点的动能，即可求出机械能的最小值。
（1）受力分析如图所示：
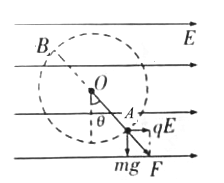
等效重力为： 
，依据几何关系可得： 
，
解得： 
由题可知： 
解得： 
．
（2）由动能定理可得： 
解得： 
（3）设圆周运动的最低点为重力势能的零点，根据动能定理： 
解得： 
故
点的机械能： 
电场力做功且做负功： 
，
故机械能的最小值为： 
练习册系列答案
口算能手系列答案
相关题目
