题目内容
（2010?四川）a是地球赤道上一栋建筑，b是在赤道平面内作匀速圆周运动、距地面9.6×106m的卫星，c是地球同步卫星，某一时刻b、c刚好位于a的正上方（如图甲所示），经48h，a、b、c的大致位置是图乙中的（取地球半径R=6.4×106m，地球表面重力加速度g=10m/s2，π=| 10 |
分析：本题主要考查同步卫星，近地卫星及赤道上的物体间的追赶问题．
对于不同轨道上的追赶问题，我们要从不同卫星的角速度或周期关系出发去解决问题．
对于不同轨道上的追赶问题，我们要从不同卫星的角速度或周期关系出发去解决问题．
解答：解：由于a物体和同步卫星c的周期都为24h．所以48h后两物体又回到原位置，故A错误；
b是在赤道平面内作匀速圆周运动、距地面9.6×106m的卫星，
根据万有引力提供向心力得：
=mr(
)2 ①
根据地球表面的物体万有引力等于重力得：
=mg ②
由①②式解得：
b卫星运行的周期T≈2×104s，
然后再算b卫星在48小时内运行的圈数n=48h/T，代入数据得n=8.64圈，
故选B．
b是在赤道平面内作匀速圆周运动、距地面9.6×106m的卫星，
根据万有引力提供向心力得：
| GMm |
| r2 |
| 2π |
| T |
根据地球表面的物体万有引力等于重力得：
| GMm |
| R2 |
由①②式解得：
b卫星运行的周期T≈2×104s，
然后再算b卫星在48小时内运行的圈数n=48h/T，代入数据得n=8.64圈，
故选B．
点评：利用题目提供的物理量找出不同卫星的角速度或周期关系，根据圆周运动知识求出转过的圈数．
运用黄金代换式GM=gR2求出问题是考试中常见的方法．
运用黄金代换式GM=gR2求出问题是考试中常见的方法．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
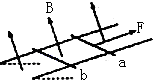（2010?四川）如图所示，电阻不计的平行金属导轨固定在一绝缘斜面上，两相同的金属导体棒a、b垂直于导轨静止放置，且与导轨接触良好，匀强磁场垂直穿过导轨平面．现用一平行于导轨的恒力F作用在a的中点，使其向上运动．若b始终保持静止，则它所受摩擦力可能（ ）
（2010?四川）如图所示，圆弧虚线表示正点电荷电场的等势面，相邻两等势面间的电势差相等．光滑绝缘直杆沿电场方向水平放置并固定不动，杆上套有一带正电的小滑块（可视为质点），滑块通过绝缘轻弹簧与固定点O相连，并以某一初速度从M点运动到N点，OM＜ON．若滑块在M、N时弹簧的弹力大小相等，弹簧始终在弹性限度内，则（ ）