题目内容
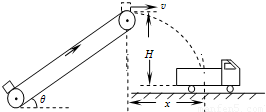
如图是利用传送带装运煤块的示意图.其中,传送带长20m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮轴顶端与运煤车底板间的竖起高度H=1.8m,与运煤车车箱中心的水平距离x=1.2m.现在传送带底端由静止释放一些煤块(可视为质点),煤块在传送带的作用下先做匀加速直线运动,后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.要使煤块在轮的最高点水平抛出并落在车箱中心,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:(l)传送带匀速运动的速度v及主动轮和从动轮的半径R
(2)煤块在传送带上由静止开始加速至落到车底板所经过的时间T.
【答案】分析:(1)根据平抛运动的高度确定平抛的时间,再根据水平位移求出平抛运动的初速度.平抛运动的初速度等于传送带匀速运动的速度v.当煤块到达轮的最高点时对轮的压力为零,煤块做平抛运动,根据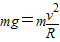 求出从动轮的半径R.
求出从动轮的半径R.
(2)根据牛顿第二定律求出煤块做匀加速直线运动的加速度,根据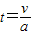 求出匀加速运动的时间,然后求出匀速运动的时间,加上平抛运动的时间,三个时间之和为煤块在传送带上由静止开始加速至落到车底板所经过的时间T.
求出匀加速运动的时间,然后求出匀速运动的时间,加上平抛运动的时间,三个时间之和为煤块在传送带上由静止开始加速至落到车底板所经过的时间T.
解答:解:(l)由平抛运动的公式,得x=vt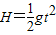
代入数据解得v=2m/s
要使煤块在轮的最高点做平抛运动,则煤块到达轮的最高点时对轮的压力为零,由牛顿第二定律,得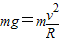
代入数据得R=0.4m
故传送带匀速运动的速度v为2m/s,从动轮的半径R为0.4m.
(2)由牛顿第二定律F=ma得
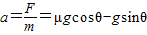 =0.4m/s2
=0.4m/s2
由v=v+at得
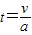 =5s
=5s
s=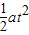 S=15m t1=
S=15m t1=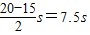
下落时需要t2=0.6s.
故总共的时间T=t+t1+t2=13.1s.
故煤块在传送带上由静止开始加速至落到车底板所经过的时间T为13.1s.
点评:解决本题的关键知道平抛运动的初速度等于传送带的速度,以及知道煤块先做匀加速运动再做匀速运动,最后做平抛运动.
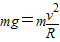 求出从动轮的半径R.
求出从动轮的半径R.(2)根据牛顿第二定律求出煤块做匀加速直线运动的加速度,根据
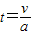 求出匀加速运动的时间,然后求出匀速运动的时间,加上平抛运动的时间,三个时间之和为煤块在传送带上由静止开始加速至落到车底板所经过的时间T.
求出匀加速运动的时间,然后求出匀速运动的时间,加上平抛运动的时间,三个时间之和为煤块在传送带上由静止开始加速至落到车底板所经过的时间T.解答:解:(l)由平抛运动的公式,得x=vt
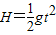
代入数据解得v=2m/s
要使煤块在轮的最高点做平抛运动,则煤块到达轮的最高点时对轮的压力为零,由牛顿第二定律,得
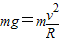
代入数据得R=0.4m
故传送带匀速运动的速度v为2m/s,从动轮的半径R为0.4m.
(2)由牛顿第二定律F=ma得
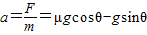 =0.4m/s2
=0.4m/s2由v=v+at得
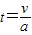 =5s
=5s s=
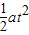 S=15m t1=
S=15m t1=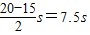
下落时需要t2=0.6s.
故总共的时间T=t+t1+t2=13.1s.
故煤块在传送带上由静止开始加速至落到车底板所经过的时间T为13.1s.
点评:解决本题的关键知道平抛运动的初速度等于传送带的速度,以及知道煤块先做匀加速运动再做匀速运动,最后做平抛运动.

练习册系列答案
相关题目
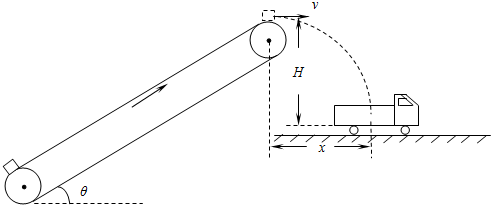
 如图是利用传送带装运煤块的示意图.其中,传送带长20m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮轴顶端与运煤车底板间的竖直高度H=1.8m,与运煤车车箱中心的水平距离x=1.2m.现在传送带底端由静止释放一些煤块(可视为质点),煤块在传送带的作用下先做匀加速直线运动,后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.要使煤块在轮的最高点水平抛出并落在车箱中心,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图是利用传送带装运煤块的示意图.其中,传送带长20m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮轴顶端与运煤车底板间的竖直高度H=1.8m,与运煤车车箱中心的水平距离x=1.2m.现在传送带底端由静止释放一些煤块(可视为质点),煤块在传送带的作用下先做匀加速直线运动,后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.要使煤块在轮的最高点水平抛出并落在车箱中心,取g=10m/s2,sin37°=0.6,cos37°=0.8,求: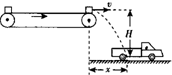 如图是利用传送带装运煤块的示意图,传送带足够长,煤块与传送带间的动摩擦因数μ=0.4,传送带与运煤车的车厢底板间的竖直高度H=1.8m,与车厢底板中心的水平距离x=1.2m,从传送带左端由静止释放的煤块(可视为质点)沿传送带先做匀加速直线运动,后随传送带一起做匀速运动,最后从右端水平抛出并落在车厢底板中心,取g=10m/s2,求:
如图是利用传送带装运煤块的示意图,传送带足够长,煤块与传送带间的动摩擦因数μ=0.4,传送带与运煤车的车厢底板间的竖直高度H=1.8m,与车厢底板中心的水平距离x=1.2m,从传送带左端由静止释放的煤块(可视为质点)沿传送带先做匀加速直线运动,后随传送带一起做匀速运动,最后从右端水平抛出并落在车厢底板中心,取g=10m/s2,求: 如图是利用传送带装运煤块的示意图,传送带足够长,煤块与传送带间的动摩擦因数μ=0.4,传送带与运煤车的车厢底板间的竖直高度H=1.8m,与车箱底板中心的水平距离x=1.2m.从传送带左端由静止释放的煤块(可视为质点)沿传送带先做匀加速直线运动,后随传送带一起做匀速运动,最后从右端水平抛出并落在车箱底板中心,取g=10m/s2,求:
如图是利用传送带装运煤块的示意图,传送带足够长,煤块与传送带间的动摩擦因数μ=0.4,传送带与运煤车的车厢底板间的竖直高度H=1.8m,与车箱底板中心的水平距离x=1.2m.从传送带左端由静止释放的煤块(可视为质点)沿传送带先做匀加速直线运动,后随传送带一起做匀速运动,最后从右端水平抛出并落在车箱底板中心,取g=10m/s2,求: