题目内容
弹簧振子以O点为平衡位置，在B、C两点间做简谐运动.在t＝0时刻，振子从O、B间的P点以速度v向B点运动；在t="0.20" s时，振子速度第一次变为-v；在t="0.50" s时，振子速度第二次变为-v.
(1)求弹簧振子振动的周期T；
(2)若B、C之间的距离为25 cm，求振子在4.0 s内通过的路程.
(1)作示意图根据题意，振子从P点出发.沿路径①达B再沿BP回到出发点P，历时0.20 s，由对称性tPB＝tBP＝0.10 s；同理，tPO＝tOP′=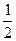
×0.30 s，故tBO=tBP+tPO=T/4.所以T＝4×(0.10+0.15) s＝1.00 s.即周期为1.00 s.
(2)
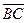="2A=25" cm，振幅A＝12.5 cm；因振子1个周期通过4A的路程，故在4.0 s＝4T内通过s＝4×4A＝200 cm.
解析
练习册系列答案
阅读快车系列答案
相关题目
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动．B、C相距20cm．某时刻振子处于B点．经过0.5s，振子首次到达C点．求：
（1）振动的周期；
（2）振子在5s内通过的路程及偏离平衡位置的位移大小．
（1）振动的周期；
（2）振子在5s内通过的路程及偏离平衡位置的位移大小．
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动，其振动图象如图所示．根据图象求：如图1所示，弹簧振子以O点为平衡位置，在A、B两点之间做简谐运动．以向左为正，振子的位移x随时间t的变化如图2所示，则由图可知（ ）
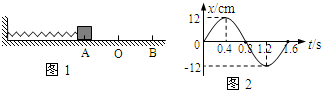
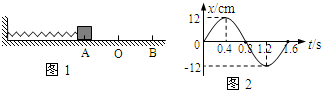
| A、t=0.2s时，振子在O点右侧6cm处 | B、t=1.4s时，振子的速度方向向右 | C、t=0.4s和t=1.2s时，振子的加速度相同 | D、t=0.4s到t=0.8s的时间内，振子的速度逐渐增大 |