题目内容
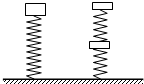（2009?孝感模拟）如图所示，一根轻质弹簧竖直放在桌面上，下端固定，上端放一重物m，稳定后弹簧长为L；现将弹簧截成等长的两段，将重物分成两块，如图所示连接后，稳定时两段弹簧的总长为L′，则（ ）分析：弹簧截成等长的两段，劲度系数变为原来的两倍，然后根据胡克定律求出各自弹簧压缩后的总长，即可比较大小．
解答：解：设弹簧原来长度为l0，劲度系数为k，则上端放一重物m，稳定后弹簧长为：L=l0-
将弹簧截成等长的两段后，劲度系数变为2k，因此稳定时两段弹簧的总长为L′=
-
+
-
=l0-
因此有：L′′＞L，故B正确，ACD错误．
故选B．
| mg |
| k |
将弹簧截成等长的两段后，劲度系数变为2k，因此稳定时两段弹簧的总长为L′=
| l0 |
| 2 |
| mg |
| 2k |
| l0 |
| 2 |
| mg |
| 2×2k |
| 3mg |
| 4k |
因此有：L′′＞L，故B正确，ACD错误．
故选B．
点评：本题关键求解出平衡位置的高度，同时注意弹簧截断后劲度系数发生变化，然后结合胡克定律求解．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
（2009?孝感模拟）一光滑圆环固定在竖直平面内，环上套着两个小球A和B（中央有孔），A、B间由细绳连接着，它们处于如图中所示位置时恰好都能保持静止状态．此情况下，B球与环中心O处于同一水平面上，AB间的细绳呈伸直状态，与水平线成300夹角．已知B球的质量为m，求：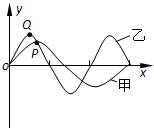
（2009?孝感模拟）如图所示为某时刻从O点同时持续发出的两列简谐横波在同一介质中沿相同方向传播的波形图，P点在甲波最大位移处，Q点在乙波的最大位移处，下列说法正确的是（ ）
（2009?孝感模拟）如图所示，空间存在相互垂直的匀强电场和匀强磁场，电场的方向竖直向下，磁场方向水平（图中垂直纸面向里），一带电油滴P恰好处于静止状态，则下列说法正确的是（ ）