Question

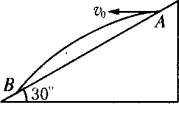
如图，AB为斜面，倾角为30°，小球从A点以初速度v₀水平抛出，恰好落到B点．求：物体从抛出开始经多长时间与斜面间的距离最大？最大距离为多少？

 

Answer 1

答案：
解析：

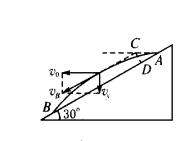
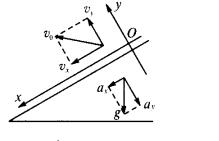
解析：当物体与斜面相距最远时，应满足该点的切线方向(即时速度方向与斜面平行，方向已知，v与水平方向成30°)由速度的分解，如图，有tan30°＝＝，所以t＝，tan30°＝． 由几何知识知，当物体速度方向与斜面平行时，物体离斜面最远，其速度方向的反向延长线交水平分位移于C，AC＝x．过C作斜面垂线，交斜面于D，则CD即为最远距离，由图可知CD＝xsin30°，水平位移x＝v0t＝，所以CD＝ACsin30°＝sin30°=． 归纳：①在平抛物体的运动中，常利用瞬时速度方向求物体的运动时间． ②恰当选择坐标轴，然后用分运动的观点和方法直接求解．对于上例，若选择沿斜面方向为x轴，垂直于斜面方向为y轴，同时分解初速度与加速度，如图，有x＝v0tcos30°＋gt2sin30°y＝v0tsin30°-gt2cos30°．利用数学知识，对y求导，y′＝v0sin30°-gtcos30°，当y′＝0时，即沿y方向速度为零时，物体离斜面最远，即v0sin30°-gtcos30°＝0，t＝tan30°，将t代入y位移表达式即得ym＝tan30°sin30°＝． 利用分运动观点，还可用动量定理和动能定理在y方向直接求解． 由动量定理：mgcos30°·t＝mv0sin30°，即物体在y方向运动最远距离所用时间t＝tan30°． 由动能定理：mgcos30°·ym＝mv02sin230°，得物体沿y方向运动的最远距离ym＝tan30°sin30°＝．