题目内容
 一列简谐横波沿x轴正方向传播,t时刻与(t+0.6)时刻的波形图正好重合,如图所示.则下列说法中正确的是( )
一列简谐横波沿x轴正方向传播,t时刻与(t+0.6)时刻的波形图正好重合,如图所示.则下列说法中正确的是( )分析:据题,t时刻与(t+0.6)时刻的波形图正好重合,经过的时间是周期的整数倍,得到周期的通项.由图读出波长,求出波速的通项,再求解特殊值.根据时间与周期的关系,分析在(t+0.4)时刻,x=-1m处的质点的状态.根据波可能的传播方向,分析从(t+0.3)时刻开始计时,x=0.5m处的质点与x=-0.5m处的质点到达波峰位置的先后.
解答:解:A、由题分析得知,nT=0.6s,n=1,2,3…,周期T=
s,所以质点振动周期不可能为1.2s.故A错误.
B、由图读出波长为λ=2m,波速v=
=
m/s=
nm/s,当n=3时,v=10m/s.故B正确.
C、t时刻到(t+0.4)时刻经过时间为0.4s,而0.4s与周期的关系为n=
=
=
n,由于n为整数,所以该时刻x=-1m处的质点不可能在平衡位置,位移不可能为零.故C错误.
D、简谐横波沿x轴正方向传播,在(t+0.3)时刻,x=0.5m处的质点振动方向可能沿y轴正方向,x=-0.5m处的质点振动方向沿y轴负方向,所以先到达波峰位置x=0.5m处的质点可能比x=-0.5m处的质点先到达波峰位置.故D正确.
故选BD
| 0.6 |
| n |
B、由图读出波长为λ=2m,波速v=
| λ |
| T |
| 2 | ||
|
| 10 |
| 3 |
C、t时刻到(t+0.4)时刻经过时间为0.4s,而0.4s与周期的关系为n=
| 0.4s |
| T |
| 0.4 | ||
|
| 2 |
| 3 |
D、简谐横波沿x轴正方向传播,在(t+0.3)时刻,x=0.5m处的质点振动方向可能沿y轴正方向,x=-0.5m处的质点振动方向沿y轴负方向,所以先到达波峰位置x=0.5m处的质点可能比x=-0.5m处的质点先到达波峰位置.故D正确.
故选BD
点评:本题考查根据数学知识列通项的能力.抓住波的周期性进行分析.波经过整数倍周期时间,图象重合;半个周期奇数倍时间,图象反相.

练习册系列答案
相关题目
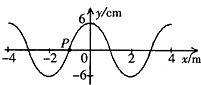 一列简谐横波沿x轴传播,t=0时刻的波形如图所示,此刻质点P正沿Y轴正方向振动.在t=0.02s时刻,质点P第一次达正向最大位移处,由此可知( )
一列简谐横波沿x轴传播,t=0时刻的波形如图所示,此刻质点P正沿Y轴正方向振动.在t=0.02s时刻,质点P第一次达正向最大位移处,由此可知( )| A、此波沿x轴正方向传播 | B、此波的传播速度为50m/s | C、从t=0起经0.04s质点P沿传播方向移动了2m | D、质点P的振动方程为y=6sin25πt(cm) |
 一列简谐横波沿x轴正方向传播,在t1=0时波传播到x轴上的质点B,在它左边的质点A恰好位于负最大位移处,如图7-2所示.在t2=0.6s时,质点A第二次出现在正的最大位移处,则( )
一列简谐横波沿x轴正方向传播,在t1=0时波传播到x轴上的质点B,在它左边的质点A恰好位于负最大位移处,如图7-2所示.在t2=0.6s时,质点A第二次出现在正的最大位移处,则( )| A、该简谐波的波速等于10 m/s | B、t2=0.6 s时,质点C在平衡位置处且向下运动 | C、t2=0.6 s时,质点C在平衡位置处且向上运动 | D、当质点D第一次出现在正最大位移处时,质点B恰好在平衡位置且向下运动 |

 (2008?绵阳模拟)一列简谐横波沿x 轴正方向以v=4m/s的速度传播,在某一时刻的波形如图所示,从图示时刻开始,经过△t=1s,x轴上的某质点P,处在x 轴下方且向+y 方向运动,则质点P距离y 轴可能是( )
(2008?绵阳模拟)一列简谐横波沿x 轴正方向以v=4m/s的速度传播,在某一时刻的波形如图所示,从图示时刻开始,经过△t=1s,x轴上的某质点P,处在x 轴下方且向+y 方向运动,则质点P距离y 轴可能是( ) 一列简谐横波沿x轴传播.T=0时的波形如图所示,质点A与质点B相距lm,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处.由此可知( )
一列简谐横波沿x轴传播.T=0时的波形如图所示,质点A与质点B相距lm,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处.由此可知( )