题目内容
如图所示，甲、乙两物体自同一水平线上同时开始运动，甲沿顺时针方向做匀速圆周运动，圆半径为R；乙做自由落体运动，当乙下落至A点时，甲恰好第一次运动到最高点B，求甲物体匀速圆周运动的向心加速度．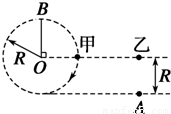
【答案】分析：根据自由落体运动求出时间，根据等时性求解周期，根据向心加速度定义公式求出向心加速度．
解答：解：设乙下落到A点的时间为t，则对乙满足R=
gt2，得t=
；
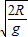这段时间内甲运动了
T，即
T=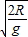
；
又由于an=ω2R=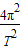
R，由①②得：an=
π2g
答：甲物体匀速圆周运动的向心加速度为
π2g．
点评：本题关键根据等时性求出运动的周期，然后根据an=ω2R求解向心加速度．
解答：解：设乙下落到A点的时间为t，则对乙满足R=
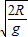gt2，得t=；这段时间内甲运动了
T，即T=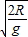；又由于an=ω2R=
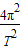R，由①②得：an=π2g答：甲物体匀速圆周运动的向心加速度为
π2g．点评：本题关键根据等时性求出运动的周期，然后根据an=ω2R求解向心加速度．
练习册系列答案
轻松暑假总复习系列答案
相关题目
（2013?淄博二模）如图所示，甲、乙两物块用跨过定滑轮的轻质细绳连接，分别静止在斜面AB、AC上，滑轮两侧细绳与斜面平行．甲、乙两物块的质量分别为m1、m2．AB斜面粗糙，倾角为α，AC斜面光滑，倾角为β，不计滑轮处摩擦，则以下分析正确的是（ ）
（2011?门头沟区一模）质量为m的物块乙以4.0m/s的速度在光滑水平面上运动，另一质量为3m的物体甲（有一轻弹簧固定其上）静止，如图所示．甲、乙两物体的运动始终在同一直线上，则下列说法正确的是（ ）
，AC斜面光滑，倾角为
，不计滑轮处摩擦，则以下分析正确的是
，则甲所受摩擦力沿斜面向上
，AC斜面光滑，倾角为
，不计滑轮处摩擦，则以下分析正确的是
，则甲所受摩擦力沿斜面向上