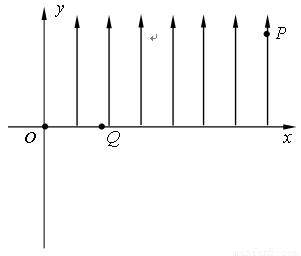
题目内容
如图所示，在纸平面内建立的直角坐标系xoy，在第一象限的区域存在沿y轴正方向的匀强电场．现有一质量为m，电量为e的电子从第一象限的某点P（L，
| ||
| 8 |
| L |
| 4 |
（1）电子经过Q点的速度v；
（2）该匀强磁场的磁感应强度B
（3）矩形匀强磁场区的最小面积S．
分析：电子在电场中做类似平抛运动，根据类似平抛运动的分运动公式列式求解末速度大小和方向；
电子进入第四象限后现在匀速运动后做匀速圆周运动，画出轨迹，找到圆心，根据几何关系列式求解出半径；然后根据洛伦兹力提供向心力列式求解磁感应强度，
最后根据轨迹得到磁场最小面积．
电子进入第四象限后现在匀速运动后做匀速圆周运动，画出轨迹，找到圆心，根据几何关系列式求解出半径；然后根据洛伦兹力提供向心力列式求解磁感应强度，
最后根据轨迹得到磁场最小面积．
解答：解：（1）做类平抛运动：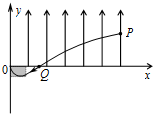
水平方向：x=
L=v0t
竖直方向：y=
L=
at2
又：a=
则：vy=at=
v0
v=
=
v0
方向：左偏下30°角
（2）由几何知识：
=R+
R=
=
得：B=
=
（3）设矩形的两个边为a、b
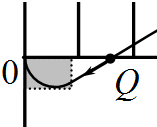
a=R
b=R+Rcos60°=
R=
s=a×b=
×
=
答：（1）电子经过Q点的速度v为
；
（2）该匀强磁场的磁感应强度B为
（3）矩形匀强磁场区的最小面积S为
．
水平方向：x=
| 3 |
| 4 |
竖直方向：y=
| ||
| 8 |
| 1 |
| 2 |
又：a=
4
| ||||
| 9L |
则：vy=at=
| ||
| 3 |
v=
|
2
| ||
| 3 |
方向：左偏下30°角
（2）由几何知识：
| L |
| 4 |
| R |
| sin30° |
R=
| L |
| 12 |
| mv |
| qB |
得：B=
| mv |
| qR |
8
| ||
| eL |
（3）设矩形的两个边为a、b
a=R
b=R+Rcos60°=
| 3 |
| 2 |
| L |
| 8 |
s=a×b=
| L |
| 12 |
| L |
| 8 |
| L2 |
| 96 |
答：（1）电子经过Q点的速度v为
2
| ||
| 3 |
（2）该匀强磁场的磁感应强度B为
8
| ||
| eL |
（3）矩形匀强磁场区的最小面积S为
| L2 |
| 96 |
点评：本题关键是找出电子的运动规律，画出轨迹图，然后分阶段根据类似平抛运动的分运动公式和洛伦兹力提供向心力列式求解．
练习册系列答案
相关题目
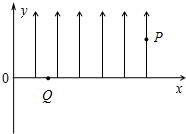如图所示，在纸平面内建立的直角坐标系xoy，在第一象限的区域存在沿y轴正方向的匀强电场．现有一质量为m，电量为e的电子从第一象限的某点P（L，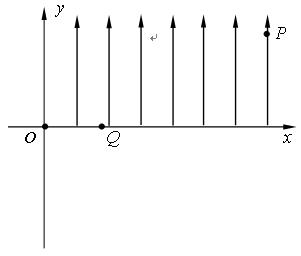
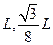）以初速度v0沿x轴的负方向开始运动，经过
轴上的点Q（
）进入第四象限，先做匀速直线运动然后进入垂直纸面的矩形匀强磁场区域，其左边界和上边界分别与y轴、x轴重合，电子经磁场偏转后恰好经过坐标原点O并沿y轴的正方向运动，不计电子的重力。求
；
；
）以初速度v0沿x轴的负方向开始运动，经过
轴上的点Q（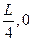
）进入第四象限，先做匀速直线运动然后进入垂直纸面的矩形匀强磁场区域，其左边界和上边界分别与y轴、x轴重合，电子经磁场偏转后恰好经过坐标原点O并沿y轴的正方向运动，不计电子的重力。求
；
；
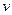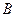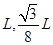）以初速度v0沿x轴的负方向开始运动，经过
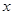轴上的点Q（
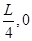）进入第四象限，先做匀速直线运动然后进入垂直纸面的矩形匀强磁场区域，其左边界和上边界分别与y轴、x轴重合，电子经磁场偏转后恰好经过坐标原点O并沿y轴的正方向运动，不计电子的重力。求
；
；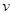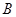