题目内容
如图甲所示,CDE是固定在绝缘水平面上的光滑金属导轨,CD=DE=L,∠CDE=60º,CD和DE单位长度的电阻均为r0,导轨处于磁感应强度为B、竖直向下的匀强磁场中。MN是绝缘水平面上的一根金属杆,其长度大于L,电阻可忽略不计。现MN在向右的水平拉力作用下以速度v0在CDE上匀速滑行。MN在滑行的过程中始终与CDE接触良好,并且与C、E所确定的直线平行。
(1)求MN滑行到C、E两点时,C、D两点电势差的大小;
(2)推导MN在CDE上滑动过程中,回路中的感应电动势E与时间t的关系表达式;
(3)在运动学中我们学过:通过物体运动速度和时间的关系图线(v-t图)可以求出物体运动的位移x,如图乙中物体在0~t0时间内的位移在数值上等于梯形Ov0Pt0的面积。通过类比我们可以知道:如果画出力与位移的关系图线(F-x图)也可以通过图线求出力对物体所做的功。
请你推导MN在CDE上滑动过程中,MN所受安培力F安与MN的位移x的关系表达式,并用F安与x的关系图线求出MN在CDE上整个滑行的过程中,MN和CDE构成的回路所产生的焦耳热。

解:(1)MN滑行到C、E两点时,在回路中的长度等于L
此时回路中的感应电动势
![]()
由于MN的电阻忽略不计,CD和DE的电阻相等
所以C、D两点电势差的大小
![]() 4分
4分
(2)设经过时间t运动到如图所示位置,
此时杆在回路中的长度
![]()
电动势
![]() 6分
6分
(3)在第(2)题图示位置时,回路中的电阻
![]()
回路中的电流
![]()
即回路中的电流为一常量。
此时安培力的大小
![]()
由于MN在CDE上滑动时的位移
![]()
所以
![]()
所以安培力的大小随位移变化的图线(F安-x图)如图所示,
所以MN在CDE上的整个滑行过程中,安培力所做的功
![]()
根据能量的转化和守恒定律
回路中产生的焦耳热Q等于安培力所做的功,即
![]() 8分
8分
 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
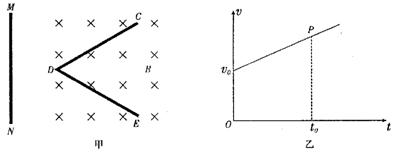
 体在0 – t0。时间内的位移在数值上等于梯形Ov0Pt的面积。通过类比我们可以知道:如果画出力与位移的关系图线(F—x图)也可以通过图线求出力对物体所做的功。
体在0 – t0。时间内的位移在数值上等于梯形Ov0Pt的面积。通过类比我们可以知道:如果画出力与位移的关系图线(F—x图)也可以通过图线求出力对物体所做的功。
