题目内容
如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为10g、电荷量为0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2T.求:
1.t=1s末速度的大小和方向;
2.1s~2s内,金属小球在磁场中做圆周运动的半径和周期;
3.在给定的坐标系中,大体画出小球在0到6S内运动的轨迹示意图。
4.6s内金属小球运动至离x轴最远点的位置坐标.
1.=
2.
m
3.
4.见解析
解析:(1)在0~1s内,金属小球在电场力作用下,在x轴方向上做匀速运动
y方向做匀加速运动 (1分)
1s末粒子的速度 (1分)
设与x轴正方向的夹角为
,则
=
(1分)
(2)在1s~2s内,粒子在磁场中做圆周运动,由牛顿第二定律
得
m (1分)
粒子做圆周运动的周期 (1分)
粒子运动轨迹如图所示 ( 2分)
(4))5s末粒子的坐标为x=v0t=6m y=at2/2=9m
此时粒子y轴方向的速度:vy=qEOt/m=6m/s
合速度大小为(2分)
第6s内粒子做圆周运动的半径( 2分)
带电粒子在第6s内做圆周运动的轨迹如图所示
第6s内粒子运动至离x轴最远点坐标为
( m ) (2分)
其中
(m ) (2分)
其中
某刻度后不动

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
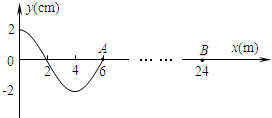
 如图甲所示,内壁光滑的绝热气缸竖直立于地面上,绝热活塞将一定质量的气体封闭在气缸中,活塞静止时处于A位置.现将一重物轻轻地放在活塞上,活塞最终静止在如图乙所示的B位置.设分子之间除相互碰撞以外的作用力可忽略不计,则活塞在B位置时与活塞在A位置时相比较( )
如图甲所示,内壁光滑的绝热气缸竖直立于地面上,绝热活塞将一定质量的气体封闭在气缸中,活塞静止时处于A位置.现将一重物轻轻地放在活塞上,活塞最终静止在如图乙所示的B位置.设分子之间除相互碰撞以外的作用力可忽略不计,则活塞在B位置时与活塞在A位置时相比较( )