题目内容
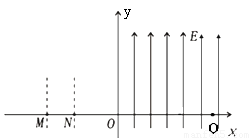
如图所示，直角坐标系的ox轴水平，oy轴竖直；M点坐标为（-0.3m，0）、N点坐标为（-0.2m，0）；在 -0.3m ≤ X ≤ -0.2m的长条形范围内存在竖直方向的匀强电场E0；在X ≥0的范围内存在竖直向上的匀强电场，场强为E=20N/C；在第一象限的某处有一圆形的匀强磁场区，磁场方向垂直纸面向外，磁感应强度B=2.5T。有一带电量q =＋1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场，恰好垂直经过y轴上的P点（图中未画出, yP>0），而后微粒经过第一象限某处的圆形磁场区，击中x轴上的Q点,速度方向与x轴正方向夹角为600。g取10m/s2。求：
1.场强E0的大小和方向；
2.P点的坐标及圆形磁场区的最小半径r；
3.微粒从进入最小圆形磁场区到击中Q点的运动时间（可以用根号及π等表示）
1.60N/C
2.0.2m
3.
【解析】（1）E0方向向上------------------①
微粒穿过MN、NO区的时间分别为t1、t2，则
---------②
---------③
过MN区加速度a竖直向上，速度变化量大小为Δv：
---------④
过NO区：
-----------⑤ 且q
E0-mg=ma-----------⑥
由① ~ ⑥得E0=60N/C------------⑦
（2）过N界偏移
------⑧
--------⑨
则
----⑩
由qE=mg------（11）得微粒飞入磁场做速度为v0的匀速圆周运动，设轨道半径为R，
由
-----（12）
--------------（13）
由几何关系得最小磁场区半径r=AC/2=R/2=0.2m-----------------------------(14)
(3)磁场中运动时间
-------------------------（15）
C~Q时间
------（16）
由几何关系得CQ=
-----（17）
-------------(18)
评分标准：每个式子各1分，共18分
鸿图图书寒假作业假期作业吉林大学出版社系列答案
（2009?宁夏）空间有一均匀强电场，在电场中建立如图所示的直角坐标系O-xyz，M、N、P为电场中的三个点，M点的坐标（0，a，0），N点的坐标为（a，0，0），P点的坐标为（a，
在如图所示的直角坐标系xyz所在的区域内，存在电场强度为E的匀强电场和磁感强度为B的匀强磁场．已知从坐标原点O沿x轴的正方向射入质子，穿过这区域时未发生偏转．设重力可忽略不计，则这区域中的E和B的方向可能是（ ）
如图所示，直角坐标系的ox轴水平，oy轴竖直；M点坐标为（-0.3m，0）、N点坐标为（-0.2m，0）；在-0.3m≤X≤-0.2m的长条形范围内存在竖直方向的匀强电场E0；在X≥0的范围内存在竖直向上的匀强电场，场强为E=20N/C；在第一象限的某处有一圆形的匀强磁场区，磁场方向垂直纸面向外，磁感应强度B=2.5T．有一带电量q=+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场，恰好垂直经过y轴上的P点（图中未画出，yP＞0），而后微粒经过第一象限某处的圆形磁场区，击中x轴上的Q点，速度方向与x轴正方向夹角为60°．g取10m/s2．求：
如图所示，直角坐标系xOy位于竖直平面内，在水平的x轴下方存在匀强磁场和匀强电场，磁场的磁感应强度为B，方向垂直xOy平面向里，电场线平行于y轴．一质量为m、电荷量为q的带正电的小球，从y轴上的A点水平向右抛出，经x轴上的M点进入电场和磁场，恰能做匀速圆周运动，从x轴上的N点第一次离开电场和磁场，MN之间的距离为L，小球过M点时的速度方向与x轴正方向夹角为θ．不计空气阻力，重力加速度为g，求：
在如图所示的直角坐标系中，第一象限内存在着一个水平宽度为L