题目内容
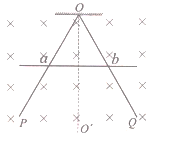
【题目】如图所示，直角三角形ABC是一个棱镜的截面，∠C=60°，MN是与棱镜的侧面AC平行的光屏，到AC的距离为L。由两种色光组成的光束宽度为d，垂直于AB射入棱镜。已知棱镜对两种色光的折射率分别为n1和n2，且n1<n2<2，求这束光经过一次折射后照射到光屏MN上的宽度。
【答案】s=
－
＋
d
【解析】
由于棱镜对两种色光的折射率不同，所以光屏上的宽度上边界按折射率小的光计算，下边界按折射率大的计算，如图所示，
设两种色光在AC面上的入射角为i，由几何关系可知i=30°，则有n1=
解得sinθ1=n1sin i=
n1
n2=
解得sin θ2=n2sin i=n2
设光照到光屏上的宽度为s，则s=Ltanθ2＋
－Ltanθ1
联立解得s=－＋d
练习册系列答案
相关题目
