题目内容
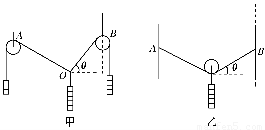
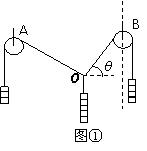
如图所示,小方块代表一些相同质量的钩码,图①中O为轻绳之间联结的节点,图②中光滑的滑轮跨在轻绳上悬挂钩码,两装置处于静止状态,现将图①中的B滑轮或图②中的端点B沿虚线稍稍上移一些,则关于θ角变化说法正确的是( )


| A、图①、图②中θ角均增大 | B、图①、图②中θ角均不变 | C、图①中θ增大、图②中θ角不变化 | D、图①中θ不变、图②中θ角变大 |
分析:根据力的平行四边形定则,结合几何关系,即可求解.
解答:解:图1中,根据钩码个数,三个力正好构成直角三角形,若端点B沿虚线稍稍上移一些,三力大小不变,根据力的合成法则,可知,方向不变,即夹角不变.
图2中,因光滑的滑轮,且绳子中的张力相等,则A、B的力总是相等的,因此合力平分A、B绳的夹角,即使稍上移,绳子张力大小仍不变,则根据力的合成法则,可知,AB夹角也不变.
故选:B
图2中,因光滑的滑轮,且绳子中的张力相等,则A、B的力总是相等的,因此合力平分A、B绳的夹角,即使稍上移,绳子张力大小仍不变,则根据力的合成法则,可知,AB夹角也不变.
故选:B
点评:本题解题关键是抓住动滑轮绳子的张力大小相等的特点,以及合力与分力的关系:合力大小不变,夹角增大时,合力减小进行分析.

练习册系列答案
相关题目