题目内容
如图所示,一对平行光滑轨道放置在水平面上,两轨道相距L=1m,两轨道之间用电阻R=2Ω连接,有一质量为m=0.5kg的导体杆静止地放在轨道上与两轨道垂直,杆及轨道的电阻皆可忽略不计,整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上.现用水平向右拉力沿轨道方向拉导体杆,使导体杆从静止开始做匀加速运动.经过位移s=0.5m后,撤去拉力,导体杆又滑行了s′=3s=1.5m后停下.求:
(1)全过程中通过电阻R的电荷量.
(2)整个过程中导体杆的最大速度.
(3)在匀加速运动的过程中,某时拉力与时间的关系式.
(1)全过程中通过电阻R的电荷量.
(2)整个过程中导体杆的最大速度.
(3)在匀加速运动的过程中,某时拉力与时间的关系式.

(1)设全过程中平均感应电动势为
,平均感应电流为
,时间为△t,
通过电阻R的电荷量为q,则
=
=
=
,
得q=
△t=
=2C
(2)拉力撤去时,导体杆的速度v即为最大速度,拉力撤去后杆运动时间为△t2,平均感应电流为
2,
根据动量定理有:B
2L△t2=mv,
即
=mv,
所以v=
=BL
q=6m/s
(3)匀加速运动过程中a=
=36m/s2
对t时刻,由牛顿运动定律得F-BIL=ma
F=ma+BIL=ma+
=0.5×36+
t=18+72t
| . |
| E |
| . |
| I |
通过电阻R的电荷量为q,则
| . |
| E |
| △φ |
| △t |
| BL(s+s′) |
| △t |
| 4BLs |
| △t |
得q=
| . |
| I |
| 4BLs |
| R |
(2)拉力撤去时,导体杆的速度v即为最大速度,拉力撤去后杆运动时间为△t2,平均感应电流为
| . |
| I |
根据动量定理有:B
| . |
| I |
即
| B2L2s′ |
| R |
所以v=
| B2L2s′ |
| mR |
| 3 |
| 4m |
(3)匀加速运动过程中a=
| v2 |
| 2s |
对t时刻,由牛顿运动定律得F-BIL=ma
F=ma+BIL=ma+
| B2L2at |
| R |
| 22×12×36 |
| 2 |

练习册系列答案
相关题目









 注入人体,
注入人体,
 D.液体表面层的分子比液体内部的分子有更大的分子势能
D.液体表面层的分子比液体内部的分子有更大的分子势能 D.超声波可以在真空中传播
D.超声波可以在真空中传播
 注入人体,
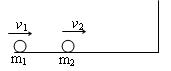
注入人体, ⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.