题目内容
甲乙两颗人造卫星绕地球做匀速圆周运动，它们的质量之比m1：m2=2：3，运行轨道的半径之比为4：9，则它们向心力之比为 ，运动的线速度之比为 ，周期之比为 ．
【答案】分析：根据万有引力提供向心力，得出线速度、周期与轨道半径的关系，从而求出向心力、线速度、周期之比．
解答：解：根据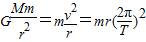
，得v=
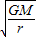，T=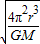
．因为轨道半径比为4：9，则线速度之比为3：2，周期之比为8：27．
向心力等于万有引力，它们的质量之比m1：m2=2：3，运行轨道的半径之比为4：9，则向心力之比为27：8．
故答案为：27：8，3：2.8：27．
点评：解决本题的关键掌握万有引力提供向心力，知道线速度、周期与轨道半径的关系．
解答：解：根据
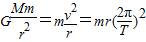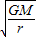，得v=，T=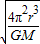．因为轨道半径比为4：9，则线速度之比为3：2，周期之比为8：27．向心力等于万有引力，它们的质量之比m1：m2=2：3，运行轨道的半径之比为4：9，则向心力之比为27：8．
故答案为：27：8，3：2.8：27．
点评：解决本题的关键掌握万有引力提供向心力，知道线速度、周期与轨道半径的关系．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
甲、乙两颗人造卫星都绕地球做匀速圆周运动，甲为地球同步卫星，乙为近地卫星．关于这两颗卫星，下列说法中正确的是（ ）
| A、甲的运行速度一定大于乙的运行速度 | B、甲的运行周期一定大于乙的运行周期 | C、甲卫星在运行时不可能经过北京的正上方 | D、两卫星的运行速度均可以等于第一宇宙速度 |