题目内容
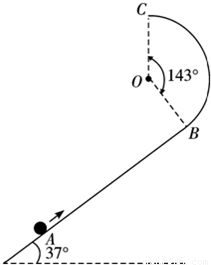
如图所示，粗糙斜面的倾角为θ=37°，斜面上方有一半径为R=1m、圆心角等于143°的竖直圆弧形光滑轨道，轨道与斜面相切于B点，轨道的最高点为C．一质量为m=8kg的小球沿斜面向上运动，到达A点时小球的动能为EKA=508J，经过B点后恰好能到达C点．已知小球与斜面间的动摩擦因数μ=3/8，重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8，求：（1）A、B两点间的距离；
（2）小球经过C点后第一次落到斜面上的位置．
【答案】分析：（1）小球在圆形轨道上做圆周运动，由向心力公式可以求出小球在C点的速度；
以小球为研究对象，由能量守恒定律可以求出A与B间的距离．
（2）小球离开圆形轨道后做平抛运动，由平抛运动的规律可以求出小球第一次落到斜面上的位置．
解答：
解：（1）小球恰好到达C点，小球在C点做圆周运动所需向心力由小球重力提供，
由牛顿第二定律可得：mg=m
①，
小球由A到C的全过程，由能量守恒定律得：
EKA=mg（ABsin37°+R+Rcos37°）+μmgcos37°×AB+
mvC2 ②，
由①②解得：AB=4.5m．
（2）作CO延长线交斜面于D点，从C点平抛后，
小球第一次落到斜面上F点，过F点作CO的垂线，与CO交于E点．
小球离开C点后做平抛运动，由平抛规律得：
水平方向：FD?cos37°=vCt ③，
竖直方向：FDsin37°+R+
=
gt2 ④，
由③④解得：FD=3.75m，而AB=4.5m，BD=0.75m，即AD=3.75m
所以A点与F点重合，小球经 C点后第一次落到斜面上的位置为A点．
答：（1）A、B两点间的距离是4.5m；
（2）小球经过C点后第一次落到斜面上的A点．
点评：本题难度较大，是一道难题，分析清楚小球的运动过程，知道小球在C点做圆周运动需要的向心力由小球重力提供是正确解题的关键；应用能量守恒定律、平抛运动的运动规律即可正确解题．
以小球为研究对象，由能量守恒定律可以求出A与B间的距离．
（2）小球离开圆形轨道后做平抛运动，由平抛运动的规律可以求出小球第一次落到斜面上的位置．
解答：
解：（1）小球恰好到达C点，小球在C点做圆周运动所需向心力由小球重力提供，由牛顿第二定律可得：mg=m
①，小球由A到C的全过程，由能量守恒定律得：
EKA=mg（ABsin37°+R+Rcos37°）+μmgcos37°×AB+
mvC2 ②，由①②解得：AB=4.5m．
（2）作CO延长线交斜面于D点，从C点平抛后，
小球第一次落到斜面上F点，过F点作CO的垂线，与CO交于E点．
小球离开C点后做平抛运动，由平抛规律得：
水平方向：FD?cos37°=vCt ③，
竖直方向：FDsin37°+R+
=gt2 ④，由③④解得：FD=3.75m，而AB=4.5m，BD=0.75m，即AD=3.75m
所以A点与F点重合，小球经 C点后第一次落到斜面上的位置为A点．
答：（1）A、B两点间的距离是4.5m；
（2）小球经过C点后第一次落到斜面上的A点．
点评：本题难度较大，是一道难题，分析清楚小球的运动过程，知道小球在C点做圆周运动需要的向心力由小球重力提供是正确解题的关键；应用能量守恒定律、平抛运动的运动规律即可正确解题．
练习册系列答案
相关题目
如图所示，受斜向上的恒定拉力作用，物体在粗糙水平面上做匀速直线运动，则下列说法中正确的是（ ）
（2011?安徽一模）如图所示，倾角为30°的光滑斜面与粗糙的水平面平滑连接．现将一滑块（可视为质点）从斜面上A点由静止释放，最终停在水平面上的C点．已知A点距水平面的高度h=0.8m，B点距C点的距离L=2.0m．（滑块经过B点时没有能量损失，g=10m/s2），求：
如图所示，同一物块分别放在水平面和固定斜面上，在两个大小相等的推力F1、F2作用下运动，F1、F2方向分别平行于水平面和斜面．若物块在推力作用下通过的位移大小相等，则推力F1、F2对物块所做的功（ ）| A、相等 | B、与物块和接触面的粗糙程度有关 | C、在水平面上推力所做的功较多 | D、在斜面上推力所做的功较多 |
如图所示，将一个质量为1kg的小物块轻轻放在倾角为37°（sin37°=0.6）的斜面上，已知斜面质量也为1kg，重力加速度为10m/s2．若斜面在足够粗糙的水平地面上没有滑动，那么地面的支持力FN和摩擦力Ff有可能为（ ）| A、FN=16.4N，Ff=4.8N | B、FN=18.2N，Ff=2.4N | C、FN=20N，Ff=0 | D、FN=20N，Ff=4.8N |
