Question

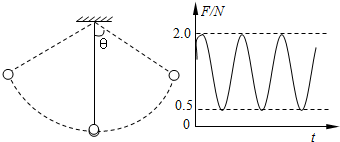
小球用一条不可伸长的轻绳相连接，绳的另一端固定在悬点上．当小球在竖直面内来回摆动（如图甲所示），用力传感器测得绳子对悬点的拉力大小随时间变化的曲线（如图乙所示）．已知绳长为1.6m，绳子的最大偏角θ=60°，g=10m/s²，试求：
（1）小球的质量m；
（2）小球经过最低时的速度v．

Answer 1

分析：（1）小球在最高点时绳子的拉力最小，在最低点时绳子拉力最大，由图读出最高点时绳子的拉力，根据最高点时向心力为0，即绳子的拉力与重力绳子方向的合力为0，列式求出摆球的质量m．
（2）根据最低点时绳子的拉力最大，结合牛顿第二定律求出摆球的最大速度．

解答：解：（1）由图读出，小球在最高点时的拉力大小 F_min=0.5N
小球在最高点时，小球的速度为0，向心力为0，即绳子的拉力与重力绳子方向的合力为0，则有：
  F_min=mgcosθ
得：m=

Fmin

gcosθ

=

0.5

10×cos60°

kg=0.1kg
（2）由图读出，小球在最低点时的拉力大小 F_max=2N
小球在最低点，根据牛顿第二定律有：F_max-mg=

mv2

r

代入数据解得：v=

Fmaxr m -gr

=

2×1.6 0.1 -10×1.6

m/s=4m/s．
答：（1）小球的质量m为0.1kg；
（2）小球经过最低时的速度v为4m/s．

点评：解决本题的关键掌握单摆的运动规律，知道单摆的周期公式，以及会灵活运用动能定理、牛顿定律解题．